神经网络优化算法技巧

在前一章的介绍中, 我们已经明白, 神经网络学习的本质是一个优化问题: 通过多轮迭代对参数进行最优化, 从而使得损失函数的值尽可能的小. 和普通的最优化问题不同, 神经网络的最优化问题涉及的参数空间复杂, 无法使用解析的方式求得最优解, 而在深度神经网络中, 参数的规模则更加庞大.

上一章中, 我们简述了随机梯度下降法作为神经网络训练过程中的参数优化方法. 在本节中, 我们将继续介绍其余几种更复杂, 性能更好的参数优化方法.

1. 随机梯度下降法 SGD

随机梯度下降法在上一章中已经简要介绍. 在介绍新方法之前, 我们先简要回顾一下:

SGD 的核心原理如下式所示:

此处, $W$ 为待更新的权重参数, $\eta$ 为每一次更新所执行的优化步长 (学习率), $\frac{\partial{L}}{\partial{W}}$ 为损失函数 $L$ 关于 $W$ 的偏导数.

其 Python 实现如下:

1
2
3
4
5
6
7
8
9
10
class SGD:
    def __init__(self, lr=0.01):
    
    # lr: learning rate, set to 0.01 here as an example

        self.lr = lr
    
    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]

SGD 的优化思想很简单: 始终认为梯度指向极值, 按照它的方向不断行进, 最后就会到达极值处. 而当函数的梯度并不和假设一样指向极值时, 其效率就会明显下降. 考虑一个曲面或超曲面, 使用 SGD 方法求其最低点时, 极有可能陷入曲面的鞍点处而难以逃脱:

下面, 我们介绍几个更优化的方法.

2. 动量方法 Momentum

动量方法是物理模型和数学意义的结合, 它将参数进行最优化的过程假定为参数取值点在高低不一的平面或超平面上运动的过程, 引入了 “动量“ 的概念, 这与其名称对应. 其核心原理如下式所示:

此处出现的新变量 $v$ 对应物体运动的速度, $\alpha$ 对应和运动方向相反的摩擦阻力, 而 $\alpha v$ 即为动量的改变量. 在动量方法的优化过程中, 参数取值点除了会逐渐向梯度所指向的方向移动外, 其来回往复的运动行为会被抑制, 而单向的运动行为会被强化, 由此可以更快地从鞍点处逃逸.

其 Python 实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Momentum:
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):

        # initialize at the begining
        # store the velocity of each params, encode as a dict
    
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)
        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            params[key] += self.v[key]

3. 自适应梯度法 AdaGrad

自适应梯度法会在学习过程中为每一个参数适当调节其学习率. 其核心原理如下:

此处的 $\otimes$ 是 矩阵乘法, 变量 $h$ 保存了对参数 $W$ 而言的, 此前学习中所有梯度的平方和. 通过在每一次更新时对学习率乘以不断减小的权值 $\frac{1}{\sqrt{h}}$, 可使学习的尺度随着学习周期的增加而减小, 从而实现学习率的衰减.

其 Python 实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class AdaGrad:
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

            # plus a small num incase overflow

4. Adam 算法

Adam 方法基本可以视为前两种方法的结合, 在此不作详细介绍.

5. 批量归一化 Batch Normalization

批标准化方法的目的是强制调整神经网络激活值的分布, 从而使各层拥有适当的广度. 它拥有增大学习率, 对初始值依赖程度低, 和可抑制过拟合的特性.

在使用批标准化方法时, 需要向神经网络中插入对数据分布进行正规化的层 (Batch Normalization), 从而实现对激活值的调整.

Batch Normalization 就是以进行学习时的 mini-batch 为基本单位, 进行使数据分布的均值为 $0$, 方差为 $1$ 的正规化. 设被正规化的输入数据的集合为 ${x_1, x_2, \cdots, x_m}$, 则有:

注: $\epsilon$ 为一个极小值, 其意义在于防止分母为 $0$ 的情况发生.

上述三式将输入数据集 ${x_1, x_2, \cdots, x_m}$ 转换为均值为 $0$, 方差为 $1$ 的数据集 ${\hat{x}_1, \hat{x}_2, \cdots, \hat{x}_m}$. 通过将该处理插入到激活函数层前或后面, 可以减小数据分布的偏向.

随后, Batch Normalization 层还会对经过正规化后的数据集 ${\hat{x}_1, \hat{x}_2, \cdots, \hat{x}_m}$ 作仿射变换:

此处 $\gamma, \beta$ 为参数, 初始值分别为 $1, 0$, 在学习过程中参数值会被调整.

6. 抑制过拟合: 正则化

发生过拟合的原因主要有两个: 模型拥有大量参数 (神经网络规模大), 和训练数据不足.

一种普遍被用于抑制过拟合的方法是 权值衰减. 它通过在学习的过程中对取值较大的权重进行 “惩罚” 来抑制过拟合. 一种常见的过拟合抑制方法是: 为损失函数加上权重的 $L2$ 范数 (平方范数), 即可抑制权重变大.

[注] $L2$ 范数是各个元素的平方和.

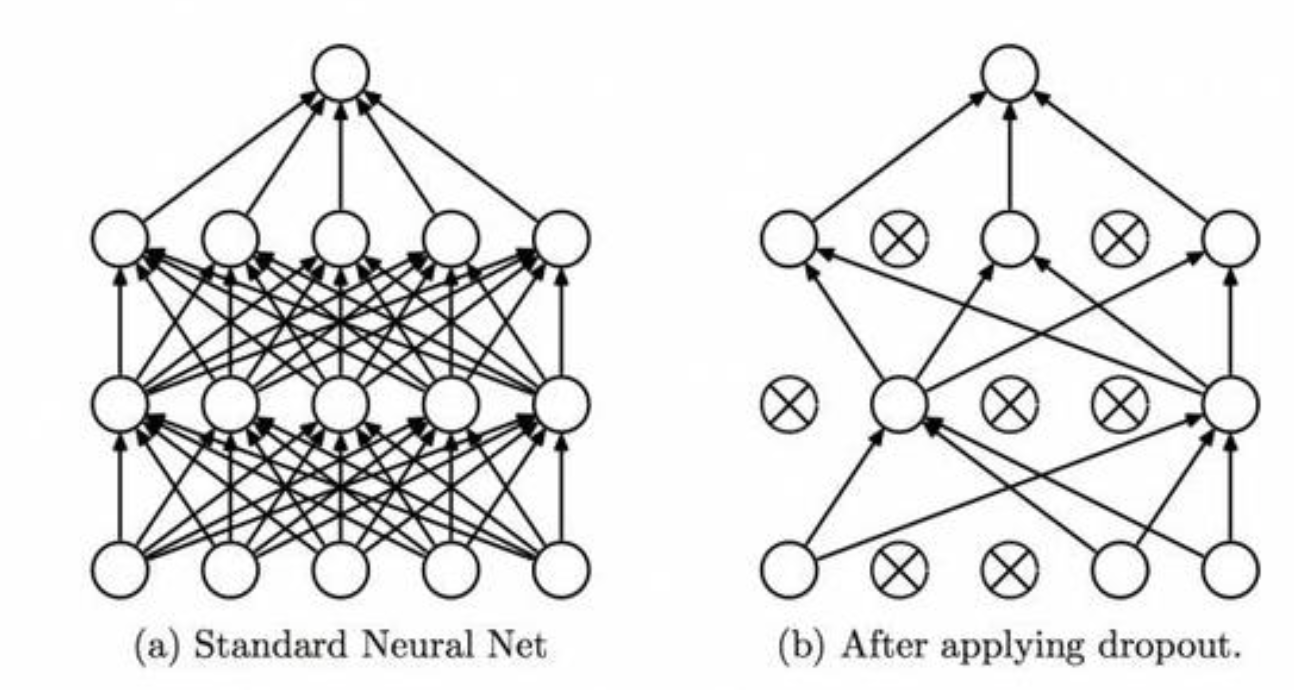
除了为损失函数加上 $L2$ 范数的权值衰减方法外, 还有一种方法可以应对复杂网络模型的过拟合抑制, 这就是 Dropout 方法.

复杂网络模型中神经元数量众多, Dropout 方法会在学习的过程中随机删除神经元. 在训练时, 随机选出隐藏层的神经元并将其删除, 被删除的神经元不再进行信号的传递.

• Previous
  从零开始的深度学习 Ch3
• Next
  从零开始的深度学习 Ch5