扩展自习 机器学习

从零开始的深度学习 Ch3

Back Propagation Algorithm

Posted by R1NG on January 9, 2021 Viewed Times

误差反向传播法

1. 反向传播

在前一章所介绍的前馈神经网络中,神经网络的输入层, 经过各个隐藏层激活函数的计算后到达输出层, 并输出结果. 在整个计算过程中, 数据始终遵循 “从前一层流动到当前层, 在当前层被处理后再流向下一层” 的流动方向, 也就是正向流动. 因此, 这样的过程也被称为 正向传播.

下面我们考虑和正向传播相对的 反向传播: 由于在不同节点处数据都被经过相较于整体而言简单一些的单独处理, 因此我们可以基于导函数计算的链式法则, 分别在每个节点处基于数据的反向流动方向, 该节点的激活函数, 以及正向传播过程中, 在该节点的输入/输出, 计算出该节点的梯度, 从而计算出损失函数值对每一个参量的梯度.

使用反向传播计算损失值关于参量的偏导数相比一阶均差法要快得多, 并且对于具有多个隐藏层的复杂神经网络, 反向传播计算法还可以计算出损失函数值关于隐藏层中参量和权值的偏导数 (数据反向流动到该隐藏层就停止, 此时的计算结果就是我们所需要的).

反向传播的基本过程是:

  1. 正向传播时, 在计算图中, 每一个计算节点保留其输入值和输出值, 并计算出该节点输出值关于输入值的偏导数, 以供在反向传播时使用该节点的局部梯度.
  2. 完成正向传播, 基于输出值和标签, 代入到损失函数中计算得到损失值.
  3. 进行反向传播: 从输出节点开始反向溯源, 对每一条数据流动路径而言, 都要将其遇到的所有节点处的局部梯度相乘, 直到反向流动至输入层, 此时其总梯度就是该参量对应的, 损失函数值对该参量的梯度.


2. 乘法层和加法层的实现

反向传播基于链式法则成立. 下面我们介绍反向传播中的乘法层和加法层, 以此深化对反向传播结构的理解.

我们首先考虑加法节点的反向传播.
以 $z = x + y$ 为对象, 观察可知其关于 $x, y$ 的偏导数均为 $1$. 这说明, 在加法节点的反向传播中, 输入值会原封不动地直接传递到下一个节点.

加法层的 Python 实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

class AddLayer:
    def __init__(self):
        pass

    def forward(self, x, y):
        out = x + y

        return out

    def backward(self, dout):
        dx = dout * 1
        dy = dout * 1

        return dx, dy


我们继续观察乘法层. 考虑 $f = x\cdot y\cdot z$, 可知: \(\frac{\partial f}{\partial x} = yz, ~~~ \frac{\partial f}{\partial y} = xz, ~~~ \frac{\partial f}{\partial z} = xy.\)

这说明, 在乘法节点的反向传播中, 输入值会被乘以正向传播时, 除去反向传播的下游方向所对应的输入信号以外, 其余所有输入信号的乘积.

乘法层的 Python 实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None

    def forward(self, x, y):
        self.x = x
        self.y = y                
        out = x * y

        return out

    def backward(self, dout):
        dx = dout * self.y
        dy = dout * self.x

        return dx, dy


3. 激活函数层的实现

下面, 我们将反向传播思想和神经网络结合, 将构成神经网络的层实现为类, 实现 ReLU 函数层和 Sigmoid 函数层:

ReLU 函数 $r(x)$:

\[r(X) = \begin{cases} x ~~~ (x > 0) \\ 0 ~~~ (x \leqslant 0)\end{cases}\]

可知其导函数为:

\[\frac{\partial r}{\partial x} = \begin{cases} 1 ~~~ (x > 0) \\ 0 ~~~ (x \leqslant 0)\end{cases}\]

可知, 对于 ReLU 函数层, 若正向传播时的输入 $x$ 大于 $0$, 则反向传播时, 会将上游的值原封不动地传递给下游, 反之来自上游的值将会停在此处, 如同一个具有记忆功能的电路开关.

ReLU 函数层的 Python 实现如下: (为确保泛用性, 此处我们将正向传播时的输入输出均视为 numpy 数组)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

class Relu:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0

        return out

    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout

        return dx

[注]
self.mask 是一个由 True, False构成的, 和 $x$ 尺寸一致的数组, 它作为 $x$ 的 “遮罩”, 将正向传播时, $x$ 的元素中全部小于等于 $0$ 的元素保存为 $True$, 其余的保存为 False. 在反向输出时, 若 self.mask 中和 $x$ 对应位置的元素为 True, 则作为输出的同尺寸数组 dout 的对应位为 $0$, 反之则为 $x$ 的对应值.


Sigmoid 函数 $S(x)$:

\[S(X) = \frac{1}{1 + \exp^{(-x)}}.\]

Sigmoid 函数的计算可基于四则运算的优先级顺序视为一个由多个节点计算所构成的计算. 其计算图如下:

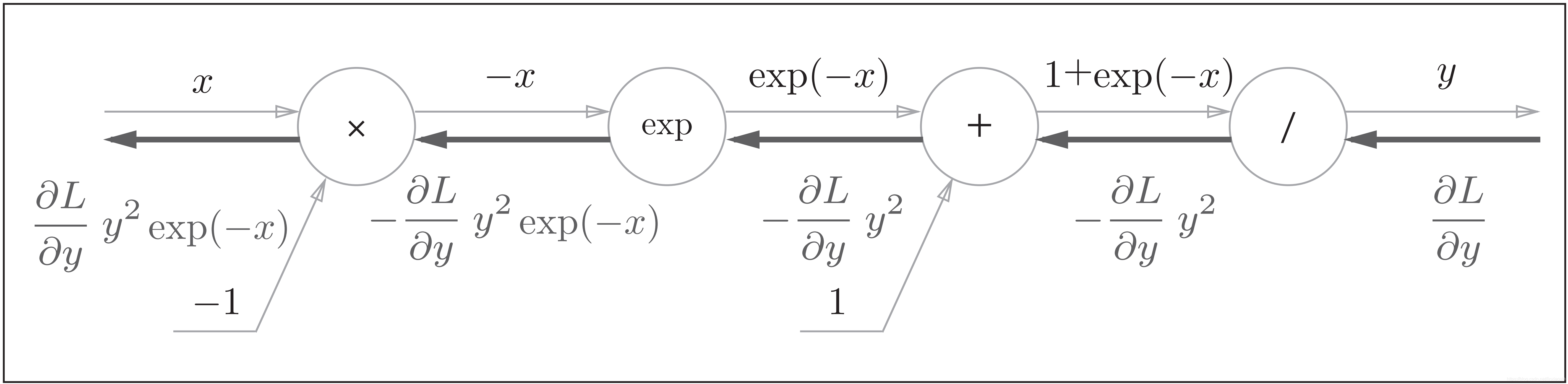
20210113100439

由计算图中的推导可知, Sigmoid 函数层的反向传播偏导函数为:

\[\frac{\partial S}{\partial x} = S(1-S).\]

Sigmoid 函数层的 Python 实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13

class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = sigmoid(x)
        self.out = out
        return out

    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out

        return dx


4. Affine/SoftMax 层的实现

下面我们分别实现 Affine 层和 SoftMax 层. 在几何意义上, 仿射变换 (Affine Transformation) 包括一次线性变换和一次平移, 对应到神经网络中就是一次加权和运算与一次加偏置运算: \(Y = X \cdot W + B.\)

在神经网络的仿射变换中, 各个节点所进行的运算都是矩阵运算. 基于矩阵的求导法则, 我们可得:

\[\frac{\partial Y}{\partial X} = W^\mathrm{T}, ~~~ \frac{\partial{Y}}{\partial W} = X^\mathrm{T}.\]

批版本的 Affine 层计算图如下图所示:

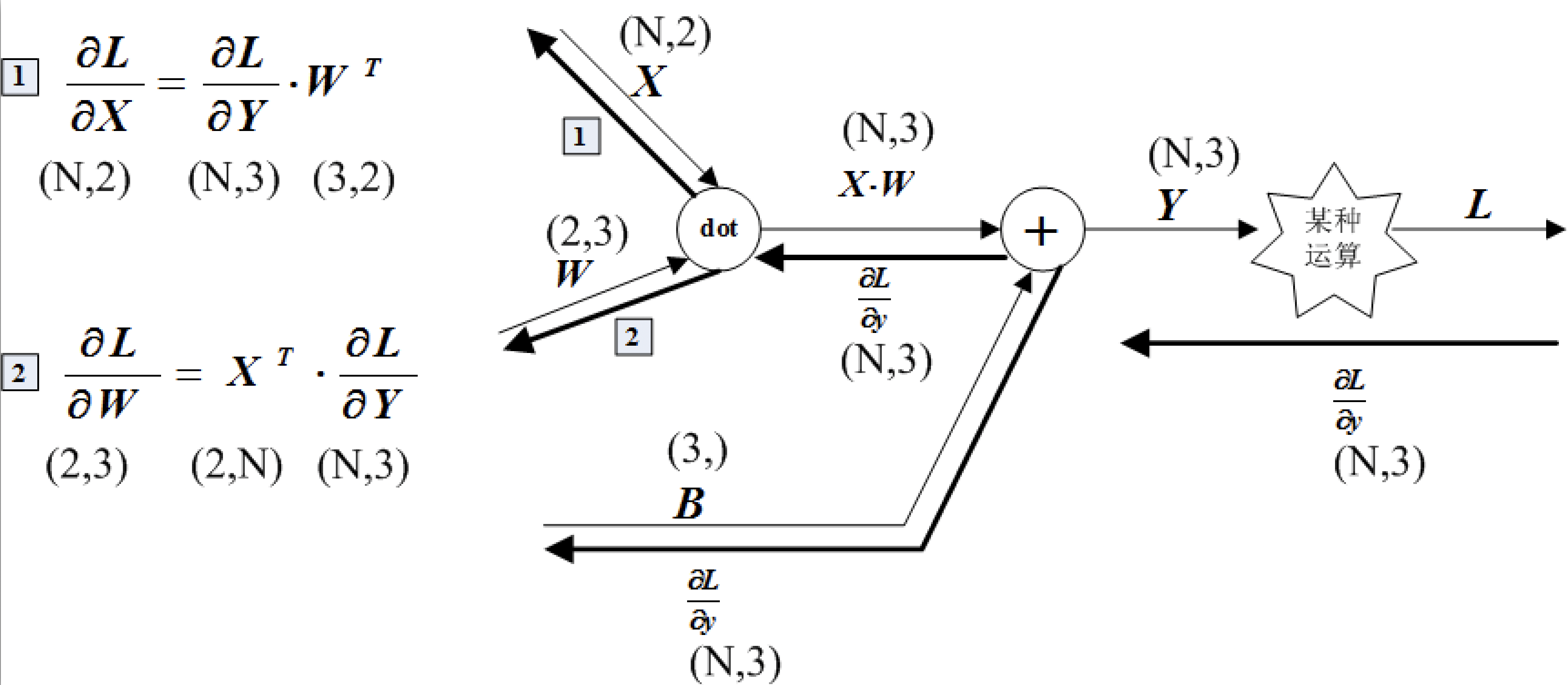
20210113102429

其 Python 实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

class Affine:
    def __init__(self, W, b):
        self.W =W
        self.b = b
        self.x = None
        self.dW = None
        self.db = None

    def forward(self, x):
        self.x = x
        out = np.dot(self.x, self.W) + self.b

        return out

    def backward(self, dout):
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)

        return dx


我们最后对 SoftMax 函数进行简要介绍. 在第一章中我们已经了解, SoftMax 函数会将输入值正规化后再输出. 考虑到 SoftMax 层同样包含作为损失函数的交叉熵误差, 因此又将其称为 SoftMax-with-Loss 层. 其计算图如下所示:

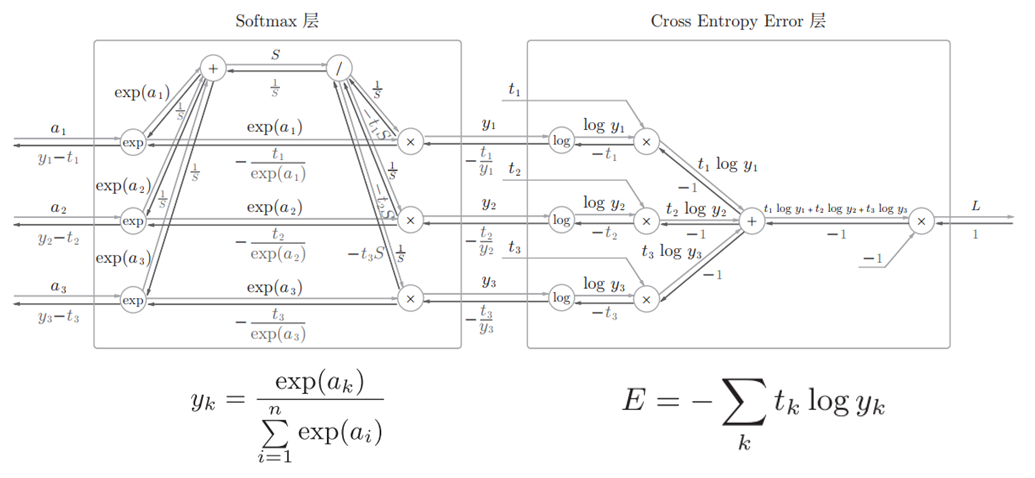
20210113105156

图中将 softmax 函数记为 SoftMax 层, 交叉熵误差记为 Cross Entropy Error 层, 并且假设进行三类分类.

其 Python 实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None # softmax的输出
        
        self.t = None # 监督数据

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        
        return self.loss

    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        if self.t.size == self.y.size: # 监督数据是one-hot-vector的情况

            dx = (self.y - self.t) / batch_size
        else:
            dx = self.y.copy()
            dx[np.arange(batch_size), self.t] -= 1
            dx = dx / batch_size
        
        return dx


5. 误差反向传播法的实现

先做一个简单的总结. 神经网络学习的全过程大致为;

  1. 从训练数据中随机选择一部分数据进行小批量学习.
  2. 计算损失函数关于各个权重参数的梯度, 误差反向传播法会在该步骤内出现.
  3. 将权重参数关于其对应梯度方向进行微小的更新.
  4. 对前三个步骤进行有限次重复.

对应误差反向传播法的神经网络的实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
        # 初始化权重

        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) 
        self.params['b2'] = np.zeros(output_size)

        # 生成层

        self.layers = OrderedDict()
        self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
        self.layers['Relu1'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])

        self.lastLayer = SoftmaxWithLoss()
        
    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)
        
        return x
        
    # x:输入数据, t:监督数据

    def loss(self, x, t):
        y = self.predict(x)
        return self.lastLayer.forward(y, t)
    
    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1 : t = np.argmax(t, axis=1)
        
        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy
        
    # x:输入数据, t:监督数据

    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)
        
        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
        
        return grads
        
    def gradient(self, x, t):
        # forward

        self.loss(x, t)

        # backward

        dout = 1
        dout = self.lastLayer.backward(dout)
        
        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 设定

        grads = {}
        grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
        grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db

        return grads

注意: 在这里, 我们将神经网络的层声明为有序字典 OrderedDict. 这使得神经网络的正向/反向传播只需按照顺序调用各层的 forward() 或 backward 方法即可.

使用误差反向传播法的学习实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

# 读入数据

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    # 梯度

    #grad = network.numerical_gradient(x_batch, t_batch)
    # 此处使用误差反向传播法计算梯度

    grad = network.gradient(x_batch, t_batch)
    
    # 更新

    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]
    
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)
    
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print(train_acc, test_acc)
CATALOG
    FEATURED TAGS
    COMP12111 课程笔记 前端学习 50P50D 大二上期末总复习 大二下期末总复习 大一上期末总复习 大三上期末总复习 人工智能 数据结构与算法 大一下期末总复习 逻辑学 高级计算机图形学 COMP15111 扩展自习 COMP21111 奇技淫巧 机器学习 计算机图形学 COMP11212 Prolog 人工智障 自然语言处理 大三下期末总复习 数据库导论 COMP15212 博弈论 数据结构和算法 数值计算方法 算法 软件工程概论 Lab
    FRIENDS