损失函数和梯度下降法
1. 基本定义和术语
机器学习是指尽可能避免人的介入, 而令程序尝试从收集到的数据中发掘模式与规律, 从而解决问题的方法. 神经网络或深度学习相比以往人为指定特征向量并使用分类器进行学习的方法, 更能避免人为介入, 通过对图像直接学习从而解决问题. 和待处理的问题无关, 神经网络可以直接将数据作为原始数据进行 “端到端” 的学习.
定义1.1: 训练数据和测试数据
训练数据 是神经网络用于学习, 寻找最优参数的数据.
测试数据 是神经网络完成学习后用于检验评价训练所得的模型的实际能力的数据.
[注]
为了正确评价神经网络训练所得模型的 泛化能力 (即所得的神经网络对新的数据有多强的处理能力), 就必须划分训练数据和测试数据. 一般地, 测试数据又成为 监督数据.
定义1.2: 过拟合
若训练出的模型仅仅对测试数据集有很强的处理能力, 而对其他不同的数据集处理能力较差的话, 则称在此次训练中出现了 过拟合 现象.
机器学习的最终目标是: 基于训练数据获得良好的泛化能力, 并最大程度地避免模型的过拟合.
定义1.3: One-Hot 表示
在神经网络的输出中, 把每一种识别结果视为一个标签, 将正确的解标签设为 $1$, 错误的设为 $0$ 的表示方法即称为
One-Hot表示.
定义1.4: 损失函数 (Loss Function)
损失函数 是表示神经网络对监督数据 不拟合 的程度, 是表示神经网络性能 恶劣程度 的指标 在训练中, 神经网络以损失函数为线索寻找最优的权重参数.
定义1.5: 小批量学习 (Mini-Batch Learning)
从海量的训练数据集中随机选出一批数据, 然后以每一批数据作为训练数据集, 进行神经网络的训练的方法称为 小批量学习.
2. 损失函数和小批量学习法
损失函数不仅是一个表示神经网络性能的指标, 它对神经网络的 “自学习” 也是至关重要的. 在神经网络的学习过程中, 寻找最优参数, 也就是权重和偏置时, 要选择一组能够使神经网络的性能相对最佳的参数, 本质上是一个优化过程: 以神经网络的参数作为待优化对象, 优化目标是使神经网络的性能相对最优. 而我们知道, 在每一步优化中, 当前的这组待优化参数需要向一个特定的方向变化, 而在梯度下降法中, 对每个参数而言, 其对应的变化方向由和它对应的损失函数的导数提供.
我们立刻注意到, 在这个优化过程中, 选择损失函数作为评价函数的重要原因是:
- 损失函数非常灵敏, 即使权值中某一个参数出现了微小变化也可能导致损失函数值的改变, 这和 “神经网络的识别正确率” 这一参数不同.
- 损失函数的变化是连续的, 其导数在定义域上不为 $0$, 以它的导数作为优化方向的指标非常可靠.
下面我们介绍两种常见的损失函数:
-
均方误差 (
\[E = \frac{1}{2}\sum_{k}(y_k - t_k)^2\]Mean Squared Error)其中, $y_k$ 表示神经网络的输出, $t_k$ 表示监督数据 (测试数据), $k$ 是数据的维度.
均方误差的
Python实现如下:1 2
def mean_squared_error(y, t): return 0.5 * np.sum((y-t)**2)
-
交叉熵误差 (
\[E = -\sum_{k}t_k\ln{(y_k)}\]Cross Entropy Error)其中, $y_k$ 为神经网络的输出, $t_k$ 为正确解标签, 且解标签中, 只有正确的值为 $1$, 其余的均为 $0$.
值得注意的是, 在交叉熵误差公式中, 实际上只会计算正确解标签的输出的自然对数. 也就是说, 交叉熵误差是由正确解标签所对应的输出结果决定的.
交叉熵误差的
Python实现如下:1 2 3
def cross_entropy_error(y, t): delta = 1e-7 return -np.sum(t * np.log(y + delta)) # prevent np.log(0) happen
我们已经知道小批量学习的定义, 通过使用 numpy 库内建的 random.choice() 函数就可以实现它:
1
2
3
4
5
train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
3. 数值微分和梯度下降法
数值微分 是一种用函数的值和其他已知信息推算该函数导数的计算方法.
在梯度下降法中, 我们使用两点估计法计算函数的一阶均差 $\frac{f(x + \Delta x) - f(x)}{\Delta x}$, 并以其近似视为函数在点 $x$ 处的导数.
由多元函数 $f(x_1, x_2, \cdots, x_n)$ 所有的偏导数 $\frac{\partial(f)}{\partial(x_i)}, ~~~ i \in [n]$ 构成的向量 $(\frac{\partial(f)}{\partial(x_1)}, \frac{\partial(f)}{\partial(x_2)} \cdots, \frac{\partial(f)}{\partial(x_n)})$ 称为这个多元函数 $f$ 的 梯度 (gradient).
对给定函数梯度的计算可以如下实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = tmp_val + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值
return grad
函数 $f(x_1, x_2) = x_1^2 + x_2^2$ 的梯度如下图所示:
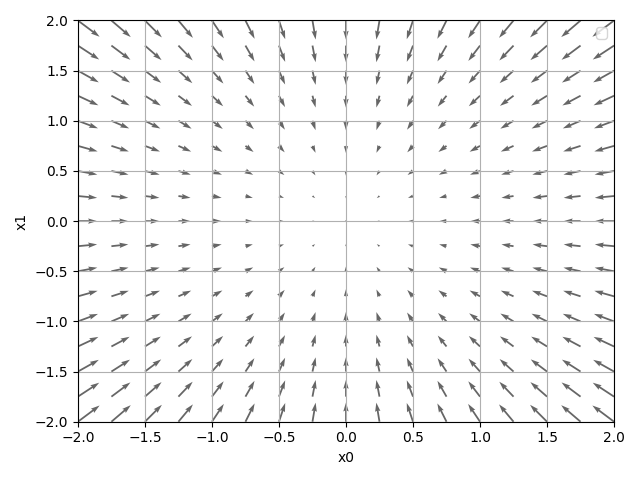
可见:
- 梯度所指示的方向是函数值减小最多的方向
- 距离局部最优点最远, 梯度值越大. (体现在箭头的长度上)
梯度下降法是一种优化方法. 在每一次优化过程中, 基于函数的当前取值, 沿其梯度方向前进给定的一段距离, 并在下一次优化过程里在新位置处重新计算梯度, 沿梯度方向继续前进. 通过不断地沿梯度方向前进, 会逐渐找到使函数值 相对最小 的参数. (思考: 为什么是 “相对最小”? 什么是 “局部最优”? 如何破解陷入局部最优的情况?)
在梯度下降法中, 每一步优化过程里前进的距离 $\eta$ 在神经网络的学习中称为 学习率. 梯度下降法的基本实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def gradient_descent(f, init_x, lr=0.01, step_num=100):
# Args:
# f: function to be learned (optimized)
# init_x: initial value
# lr: learning rate
# step_num: the number of iterations (learn how many times)
x = init_x
for i in range(step_num):
grad = numerical_gradient(f, x)
x -= lr * grad
return x
神经网络的梯度是指神经网络中损失函数关于权重参数的梯度:
[例]
神经网络 SimpleNet 的权重 $W$ 大小为 $2 \cdot 3$, 损失函数为 $L$. 则其梯度 $\frac{\partial(L)}{\partial(W)}$ 为:
其中 \(W = \begin{pmatrix} w_{11}, w_{12}, w_{13} \\ ~~ \\ w_{21}, w_{22}, w_{23}\end{pmatrix}\)
对其求梯度的 Python 实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
class simpleNet:
def __init__(self):
self.W = np.random.randn(2,3)
def predict(self, x):
return np.dot(x, self.W)
def loss(self, x, t):
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return loss
4. 随机梯度下降法的实现
先做一个简单的总结: 神经网络的随机梯度下降法学习步骤基本如下:
- 从训练数据中随机抽出一部分, 称其为
mini-batch. 学习的目标是优化参数, 尽可能地使mini-batch的损失函数最小化. - 求出各个权重参数的梯度
- 将权重参数沿梯度方向进行更新
- 重复上述步骤, 直到重复次数达到设定值.
下面, 我们实现一个功能为识别手写数字, 使用 MNIST 数据集进行学习的 $2$ 层神经网络 Two Layer Net:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
# x:输入数据, t:监督数据
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# x:输入数据, t:监督数据
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self, x, t):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# forward
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
# backward
dy = (y - t) / batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy, axis=0)
da1 = np.dot(dy, W2.T)
dz1 = sigmoid_grad(a1) * da1
grads['W1'] = np.dot(x.T, dz1)
grads['b1'] = np.sum(dz1, axis=0)
return grads
