扩展自习 机器学习

从零开始的深度学习 Ch1

Perceptron & Neural Network

Posted by R1NG on January 8, 2021 Viewed Times

感知机与神经网络

1. 感知机的定义

动物的神经系统中最基础的组成单元为神经元 (神经细胞), 用于接受刺激, 产生兴奋并传导兴奋. 神经元有且只有激活态和非激活态两种状态, 并且只有神经元处于激活态时, 传入的兴奋才会由它传出.

感知机是神经网络最基本的组成单元, 其本质是以特征向量为自变量的分段函数, 能够完整地模拟神经元的逻辑功能.

一个标准的感知机包含以下三个组成部分:

  1. 输入 (Input)
  2. 与每一个输入所对应的权值 (Weights)
  3. 激活函数 (Function)

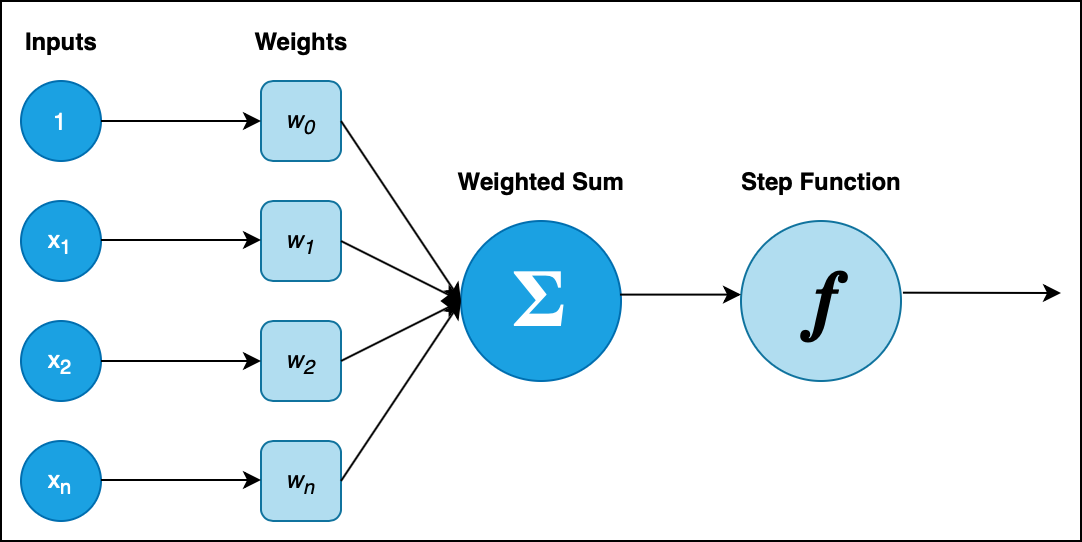
perceptron

我们定义:

\[X = (1, x_1, \cdots, x_n),~~ W = (w_0, w_1, \cdots, w_n).\]

其中, $X$ 为激活函数的输入, $W$ 为权值. 则激活函数形为:

\[f(X) = \begin{cases} 0 ~~~~~~ X \cdot W^T \leqslant \theta \\ 1 ~~~~~~ X \cdot W^T > \theta \end{cases}\]

其中, $\theta$ 称为激活函数 $f$ 的 阈值. 函数的分段条件可被转为 $X \cdot W^{T} + b ~~~(b = -\theta)$. 称 $b$ 为 偏置, 控制该感知机被激活的难易程度, $W$ 为 权重. 控制各个变量的重要程度.

不难看出, 激活函数 $f$ 是一个线性分段函数, 该函数的行为可看作对一个二维平面使用一条直线进行分割. 激活函数的线性性质决定了它无法对二维平面进行较复杂 (非线性) 的分割, 这一问题在我们使用感知机处理某些分类问题时会立即凸显, 比如使用感知机实现异或逻辑门. 首先, 我们来看几个简单的例子:

[例] 使用感知机实现与, 或, 与非门:

与, 或, 与非门的真值表如下:

$x_1$ $x_2$ AND OR NAND
$1$ $1$ $1$ $1$ $0$
$1$ $0$ $0$ $1$ $1$
$0$ $1$ $0$ $1$ $1$
$0$ $0$ $0$ $0$ $1$ 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

import numpy as np


def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

将与门, 或门, 与非门的两个输入 $x_1, x_2$ 视为平面直角坐标系的两轴, 将平面上的点视为所定义的逻辑门函数的两个输入, 可以看出: 对于上述的三种逻辑门电路而言, 其输入-输出分别将平面划分为了两个部分, 且这样的划分是线性的.


2. 感知机的局限性和扩展的多层感知机: 以异或门电路的实现为例

下面, 我们以异或门电路的分析和实现说明感知机 (单层感知机) 的局限性.

异或逻辑门的真值表如下:

$x_1$ $x_2$ XOR
$1$ $1$ $0$
$1$ $0$ $1$
$0$ $1$ $1$
$0$ $0$ $0$

实际上, 我们并不能使用单层感知机实现异或逻辑门. 不妨这样思考: 假定我们使用单层感知机实现了一个异或逻辑门函数 XOR(x_1, x_2), 则它在几何意义上必定是一个使用线性函数对二维平面的二分. 而在平面上描点观察可知, 我们并不能使用线性函数对其基于函数输出的不同而进行分割 (即将所有的红色点和蓝色点分隔开). 因此由矛盾推出, 单层感知机无法实现异或逻辑门:

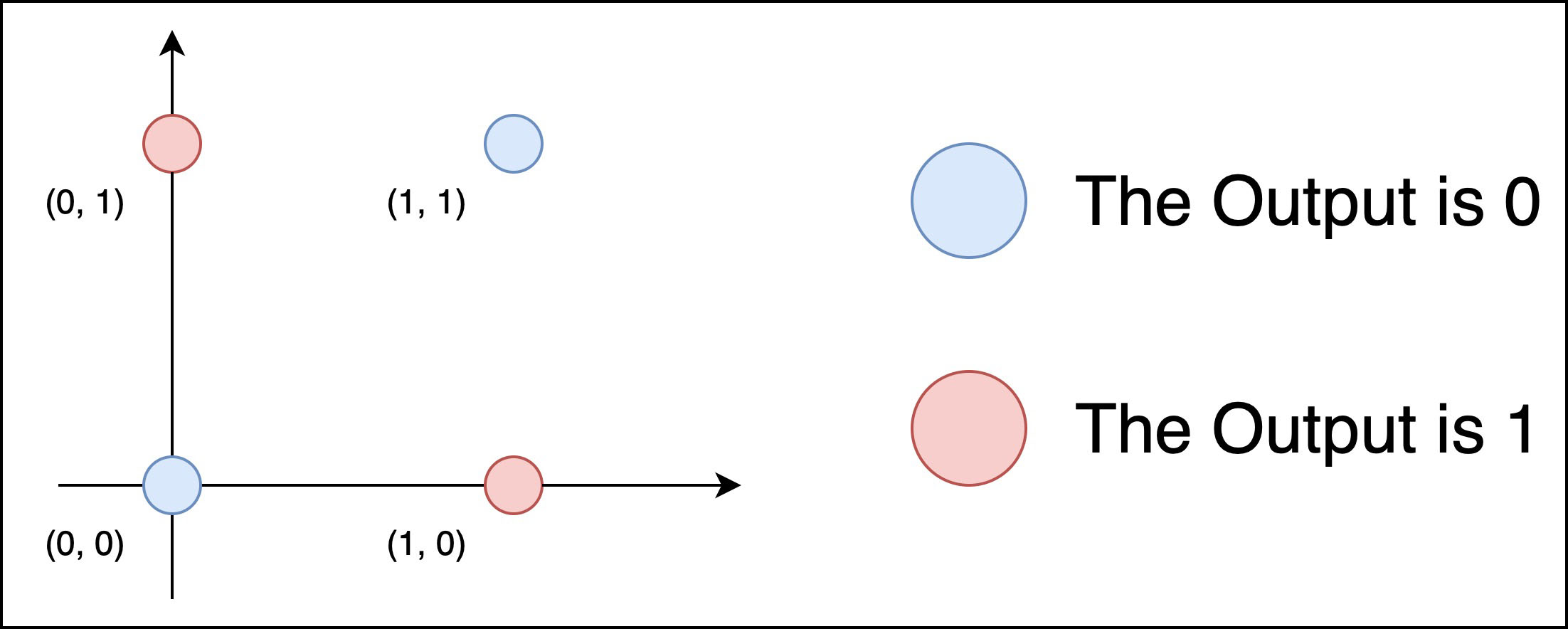
xor-gate

不过, 我们可以使用多层感知机的叠加层实现对该平面的分割. 简单推导逻辑表达式可知:

$\mathbf{XOR}(x_1, x_2) = \mathbf{AND} (\mathbf{NAND}(x_1, x_2), \mathbf{OR}(x_1, x_2))$

使用之前定义的与门, 或门和与非门就可以这样实现异或门:

1
2
3
4
5

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

形如异或门这样, 叠加了多层的感知机称为 多层感知机 (Multi-layered Perceptron). 在我们的例子中, 异或门由两级含有权重的层和一级输出层组成. 通过叠加层, 感知机可以进行更为灵活的数据分类和表示.


3. 神经网络的定义和层级结构

感知机可以通过多层叠加表示复杂函数, 适应多种分类问题. 但感知机的权重需要人为设定, 而且不同的权重会影响感知机的分类表现. 神经网络的作用是自动地从数据中 “学习” 并更新到合适的权重参数.

如下图所示, 神经网络一般有三种分层: 输入层, 中间层 (隐藏层) 和输出层. 神经网络的结构和多层感知机所组成的网络没有区别, 但其本质差异是: 神经网络采用连续函数而非线性分段函数作为激活函数.

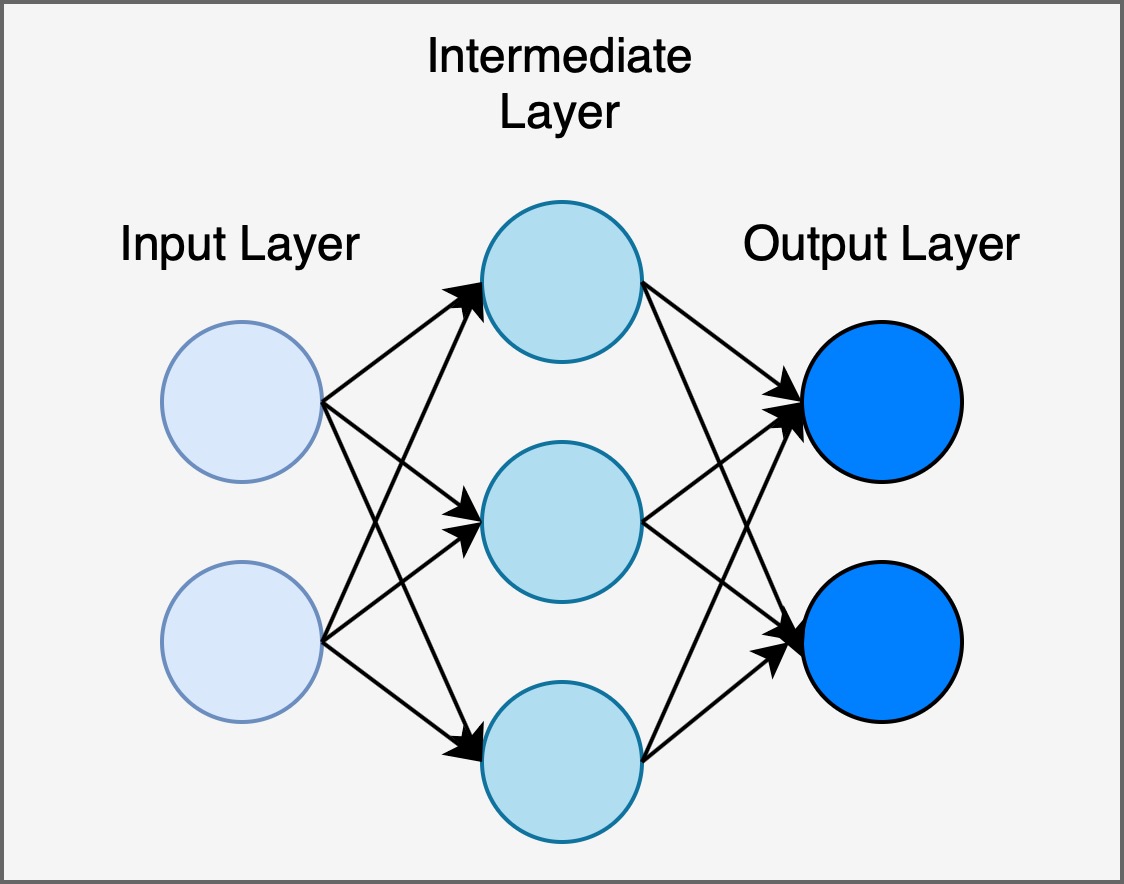
neural-network-diagram


4. 激活函数的定义和常见的激活函数

在介绍感知机时我们已经了解, 激活函数接收所有的输入信号, 并将输入信号的总和转换为输出信号, 而其核心作用在于决定如何激活输入信号的总和. 下面, 我们介绍数个常用的神经网络激活函数:

  1. Sigmoid 函数
    Sigmoid 函数 $S(x)$:

    \[S(X) = \frac{1}{1 + \exp^{(-x)}}.\]

    在 Python 中, Sigmoid 函数实现如下:

    1
2
3
4

     import numpy as np

 def sigmoid(X):
     return 1/ (1 + np.exp(-x))


  2. ReLU 函数
    ReLU 函数 $r(x)$:

    \[r(X) = \begin{cases} x ~~~ (x > 0) \\ 0 ~~~ (x \leqslant 0)\end{cases}\]

    在 Python 中, ReLU 函数实现如下:

    1
2
3
4

     import numpy as np

 def relu(X):
     return np.maximum(0, x)


  1. softmax 函数
    softmax 函数 $s(x)$:

    \[S(x) = \frac{\exp(a_k)}{\sum_{1}^{n}exp(a_i)}\]

    需要注意的是, softmax 函数的实现中涉及指数函数计算, 而在指数函数值过大时可能会溢出为 inf. 若分子和分母均溢出的话, 就无法正常地进行除法运算.

    要解决这一问题, 我们对 softmax 函数作如下修正:


    \[m = \max(a_1, a_2, \cdots, a_n)\] \[S_1(x) = \frac{\exp(a_k - m)}{\sum_{1}^{n}exp(a_i - m)}\]


    这样, 就在不改变运算的结果 (思考一下: 为什么?) 的情况下, 实现了函数的修正. 合理的 Python 实现如下:

    1
2
3
4
5
6
7
8
9

     import numpy as np

 def softmax(a):
     c = np.max(a)
     exp_a = np.exp(a - c)
     sum_exp_a = np.sum(exp_a)
     y = exp_a / sum_exp_a

     return y

    softmax 函数的一个有趣的特性是, 对任何输入值, 其函数值均在 $0, 1$ 之间, 且输出总和为 $1$. 基于这个性质, 我们可以将函数的输出解读为概率, 并用概率的工具和方法处理问题.


神经网络在解决不同类型问题, 如分类问题或回归问题 (预测问题)上时, 需要基于问题类型相应地选择输出层的激活函数. 一般地, 回归问题要用恒等函数, 而分类问题使用 softmax 函数.


5. 三层神经网络的实现

下面我们实现连接结构如下图所示的 $3$ 层神经网络:

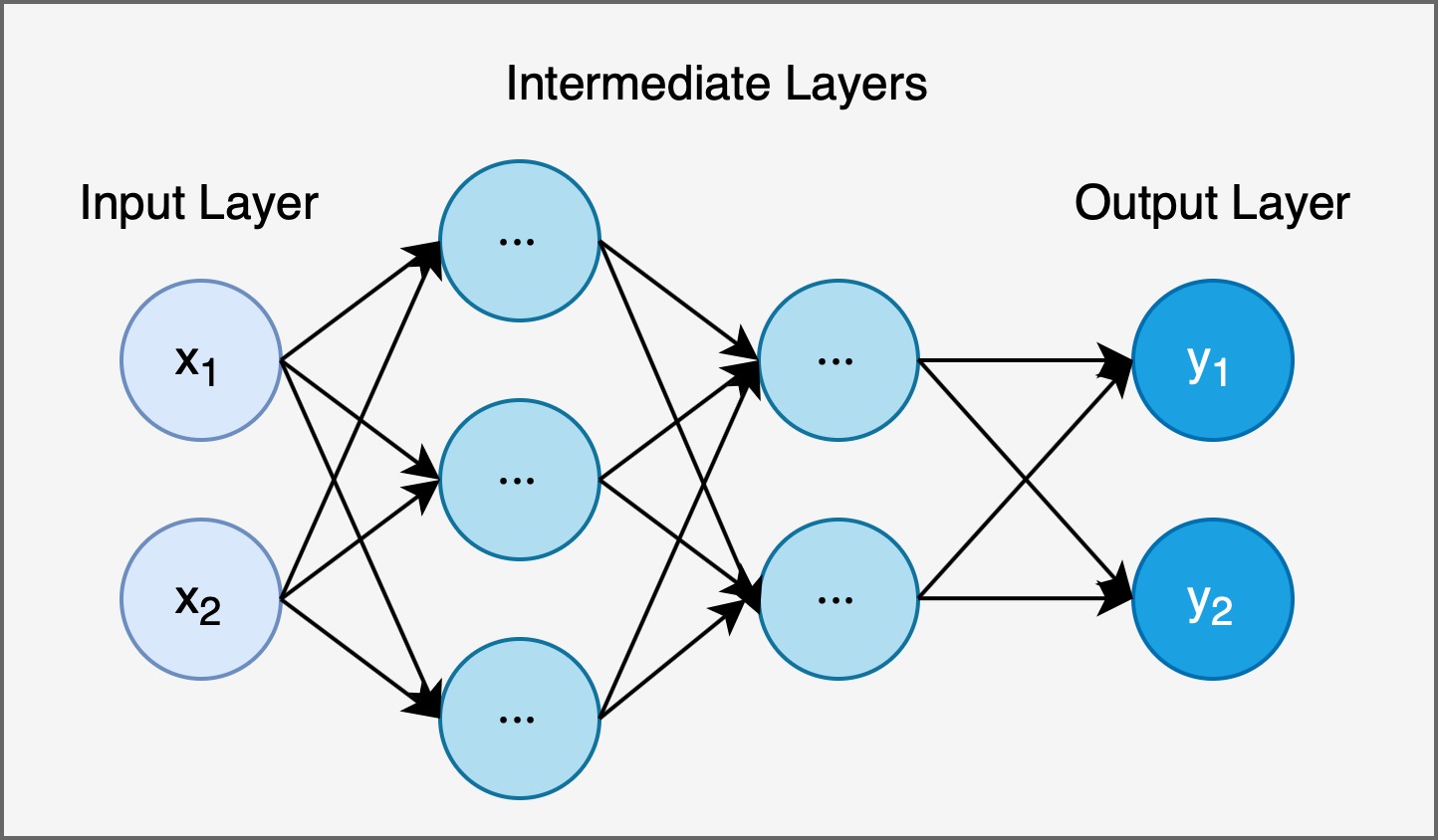
3-layers-neural-network

为了分辨复杂的层间连接, 我们引入下图所示的记号方法:

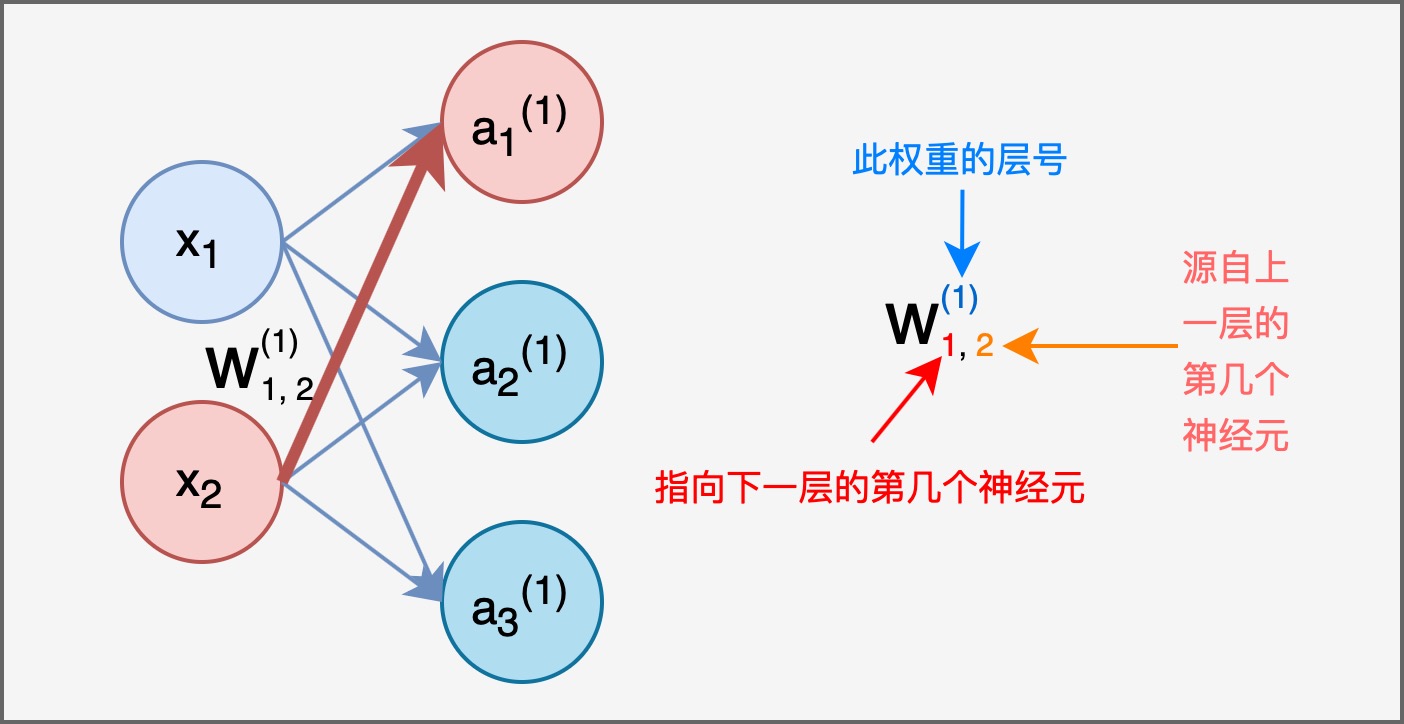
3-layers-neural-network-notations

在本例中, 我们在全部两层中间层处均使用 softmax 函数作为激活函数, 在输出层采用恒等函数作为激活函数. 并且为了更好地表示偏置, 我们在每一层都添加了一个用于表示偏置的 偏置神经元, 其输入恒为 $1$, 且不和任何其他层连接.

基于以上的连接结构和记号, 对于中间层的第一层, 我们有:

\[a_{1}^{(1)} = w_{11}^{(1)}x_1 + w_{12}^{(1)}x_2 + b_1\]

推广到全部的三个加权和, 有:


\[A^{(1)} = (a_{1}^{(1)}, a_{2}^{(1)}, a_{3}^{(1)}), ~~~ X = (x_1, x_2), ~~~ B^{(1)} = (b_{1}^{(1)}, b_{2}^{(1)}, b_{1}^{(3)})\] \[W^{(1)} = \begin{pmatrix} w^{(1)}_{11}, w^{(1)}_{21}, w^{(1)}_{31} \\ ~ \\ w^{(1)}_{12}, w^{(1)}_{22}, w^{(1)}_{32} \end{pmatrix}\] \[A^{(1)} = XW^{(1)} + B^{(1)}\]


而被激活函数转换后所得的信号 $Z_1 = \mathbf{Sigmoid}(A^{(1)}).$

我们可以将该实现方式进一步推广至全部层, 这样就实现了三层神经网络的设计. 其 Python 实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

from functions import sigmoid, identity_function
import numpy as np

def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3)
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2)
    network['W3'] = np.array([[0.1, 0.3] ], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2)
    
    return network

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)

    return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)    #the output should be [0.31682708 0.69627909]


6. 神经网络的输出

我们使用 MNIST 手写数字图像数据集, 以一个识别手写数字的三层神经网络为例简介神经网络的输出.

MNIST 的图像数据为 $28$px * $28$px 的灰度图像. 依照图片所包含的像素数量和我们需要识别的数字种类, 确定神经网络的输入层有 $784$ 个神经元, 输出层有 $10$ 个神经元. 其隐藏层又由 $50$ 个神经元构成的第一隐藏层和 $100$ 个神经元构成的第二隐藏层组成. 在原书提供的源代码中, 提供了现成的 MNIST 数据集抓取和转换函数, 而神经网络的权值保存在 sample_weight.pkl 这个 Pickel 文件中, 在定义神经网络时被直接读取.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定

import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax


def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test


def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    return network


def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)

    return y


x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
    y = predict(network, x[i])
    p= np.argmax(y) # 获取概率最高的元素的索引
    
    if p == t[i]:
        accuracy_cnt += 1

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

在执行上述代码后, 可见 Console 输出:

1

Accuracy:0.9352

可见这个处理 MNIST 数据集的神经网络已经成功运行, 并具有 $93.52\%$ 的识别精度.

CATALOG
    FEATURED TAGS
    COMP12111 课程笔记 前端学习 50P50D 大二上期末总复习 大二下期末总复习 大一上期末总复习 大三上期末总复习 人工智能 数据结构与算法 大一下期末总复习 逻辑学 高级计算机图形学 COMP15111 扩展自习 COMP21111 奇技淫巧 机器学习 计算机图形学 COMP11212 Prolog 人工智障 自然语言处理 大三下期末总复习 数据库导论 COMP15212 博弈论 数据结构和算法 数值计算方法 算法 软件工程概论 Lab
    FRIENDS