Ch5 内存模型简介
在本章中, 我们将对内存和存储进行介绍:
- 内存寻址和解码器
- 内存层级架构
- 寄存器内存
- 缓存
SRAM和DRAM
1. 内存寻址和解码器
内存用于存储计算机所需要执行的程序或数据, 可以被处理器直接访问. 在不同架构的计算机中, 内存的作用各有不同:
von Neumann架构 又称为Prineton架构, 是一种将程序指令存储器和数据存储器合二为一的计算机设计架构. 结构简单, 但存在性能瓶颈.Harvard架构 程序指令和数据被分别存储在不同的存储器中. 其优势在于数据和指令的读写可以同时进行. 并且指令和数据的数据宽度可以不一致. 但其结构更为复杂.
1.1 计算机的内存寻址空间
计算机的寻址空间内一般会将随机存储器 (Random Access Memory, RAM) 包含在内. 随机存储器中的任何位置在任何时间都可以被使用.
以 $32$ 位 ARM 架构为例: 该架构定义了 $32$ 位的寻址空间, 其中使用和涉及的绝大多数数据长度均为 $4$ 个字, 即 $32$ Bits, $4$ Bytes, 因此该架构下的随机存储器往往会同时并行访问四个位 (Bytes). 因此我们也可以将 ARM 架构的寻址空间视为 $30$ 位的, 预留出来的两个位用于标记所并行访问的四个位中的其中一个.
这样的 $30$ 位寻址空间可以访问大约为 $1Gbit$ 的数据. 在内存芯片单体容量仍然有限的时代, 要制造出能够充分利用 $32$ 位 ARM 架构寻址能力的内存, 就需要结合多块内存芯片. 内存访问时间和内存周期时间等参数都是刻画内存性能的重要指标.
1.2 内存读写和三态缓冲器
要对内存进行读写, 处理器需要通过内存访问界面向内存提供以下信息:
- 所要求执行的操作类型 (读/写)
- (若要执行写操作) 所需要被写入内存的数据
- (若要执行读操作) 所将要被读取的内存地址
需要注意的是: 由于内存不能并行执行多个操作, 因此内存的控制信号和数据总线是被整个内存所共享的.
三态缓冲器 (Tri-state Buffer) 是一隔具有两个输入信号和一个输出信号的逻辑设备. 其状态除了高电平/低电平外, 还有 高阻态.
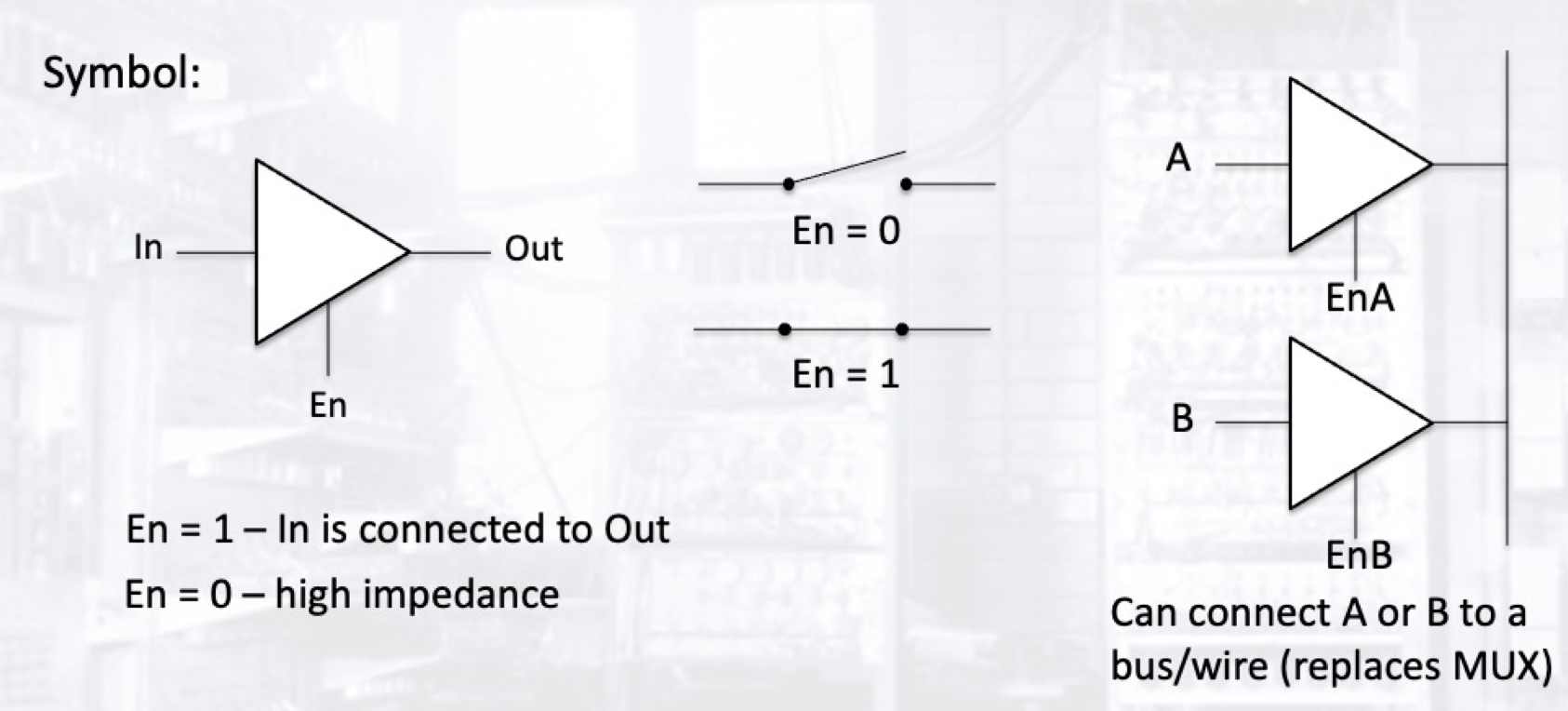
三态缓冲器本质上可被视为一个开关. 当输入 En 为高电平时, 开关闭合并将输入信号 In 直接传递至 Out, 此时该三态缓冲器的状态即和 In 一致, 而 En 为低电平时开关断开, 我们将此时的三态缓冲器状态视为高阻态.
三态缓冲器可用于控制处于同一条链路上的不同设备, 并且常用于总线的控制和切换. 一个简单的例子即为: 使用三态缓冲器构造双向数据总线:
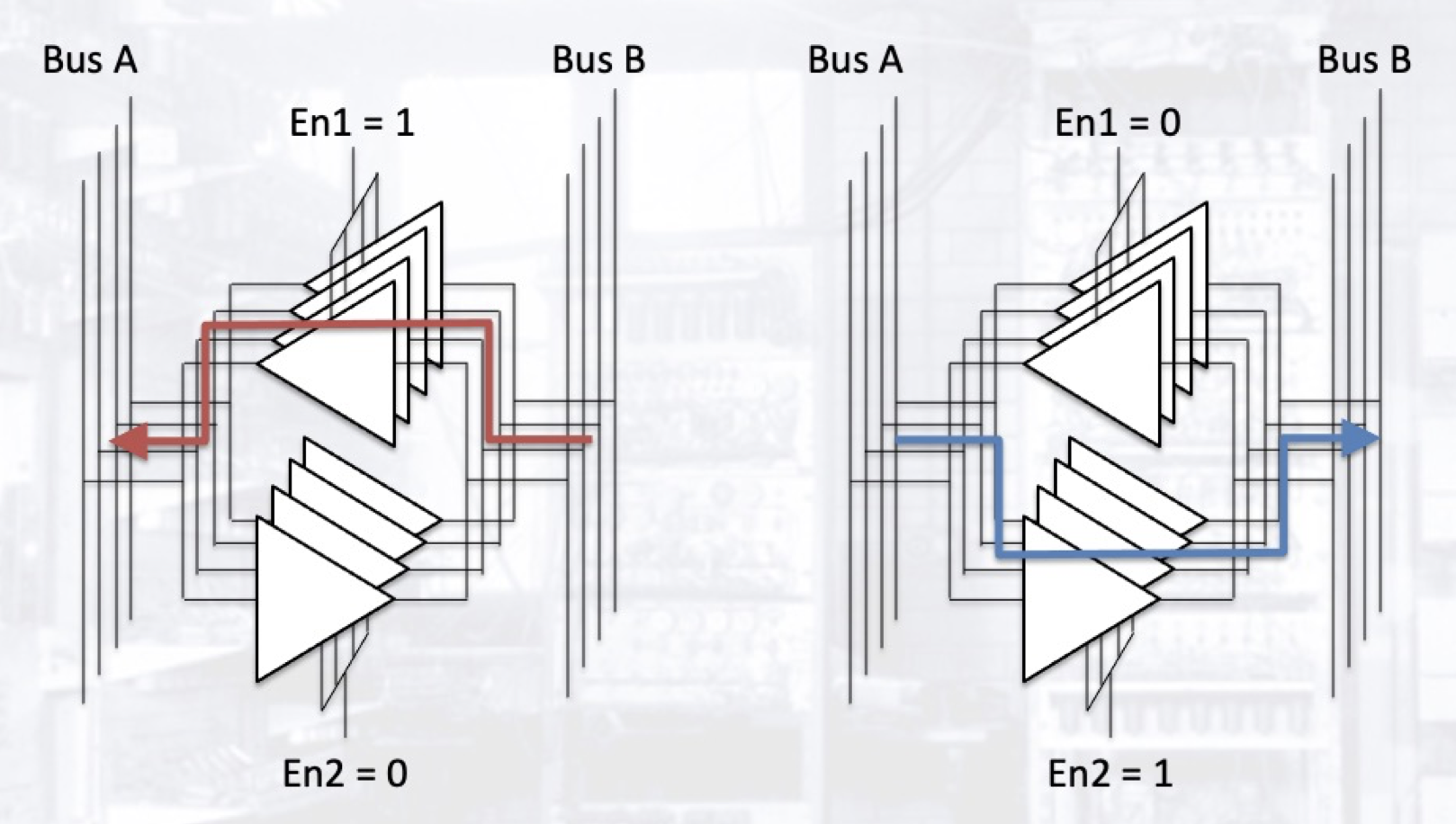
1.3 内存解码器
内存需要具备能够将处理器传递的内存地址转译并识别其实际位置的能力. 在内存中, 相应的工作需要解码器来完成.
对于一个位宽为 $n$-bit 的内存硬件而言, 其解码器需要将 $n$ 位的二进制数值解码为 $2^n$ 条输出信号中与之对应的那一条.
解码器通常用于解码用于启用不同内存块的信号. 其中较低的地址线是所有块通用的, 但较高的地址线需要被解码以确定所需要的内存位置位于哪个内存块. 对于容量较大的内存而言, 使用单个解码器对整个地址总线进行解码由于电路复杂度的问题, 往往是不切实际的. 在这种情况下, 行之有效的解决办法是仿效多位行波进位加法器的构造, 使用层级电路解决问题.
和三态缓冲器类似, 解码器也有一个输入信号控制其开闭. 当该信号为低电平时, 其输出恒为 $0$, 只有该信号为高电平时解码器才会工作. 这为我们使用层级电路设计思想构造复杂的内存解码器提供了便利.
考虑使用层级电路思想设计一个 $6-64$ 解码器: 我们将使用 $8$ 个 $3-8$ 解码器. 在这一情形下, 解码较低位的 $3-8$ 解码器的三个最高输出位将作为下一个 $3-8$ 解码器的输入. 通过这样的方式构造地址链路, 我们即可搭建出所需要的解码器.
在将内存地址解码之后, 内存需要按需访问该内存地址所映射的内存位置. 在内存中, 内存位置的排列一般有两种方式:
- 一维数组:
实际存储数据的内存位置 (块) 依序排列形成逻辑上的一维数组, 只需要一根控制信号总线即可实现对所有内存位置的访问, 但不适用于大容量内存, 因其单维度的内存位置访问方式对控制信号总线的位宽的要求极大, 所需的解码器电路也更复杂. - 二位数组:
为每一个实际存储的内存位置赋予行编号和列编号, 依序排列形成逻辑上的二位数组 (矩阵), 需要两根控制信号总线, 但在内存容量较大的情况下相比一维数组排列方式有极其明显的优势, 只需要两根位宽较小的控制信号总线即可实现对所有内存的访问.
2. 内存层级架构
自存储器诞生以来, 设计者就不得不在 容量, 读写速率和价格 上进行妥协和权衡: 同时满足高容量, 高读写速率和低价的存储设备是不存在的. 为了在这样的约束条件下实现足够优秀的性能, 我们必须引入 内存层级架构 的概念:
若从访问速度最慢的 “主存” 中执行计算机程序, 则 “主存” 的速度就会成为程序执行速度的瓶颈. 然而, 大部分的计算机程序设计思想 (如顺序访问, 循环等) 天然地和 局部性 有着良好的相性. 通过将程序中最关键的一小部分代码放到访问速度相对最快的存储介质中运行, 就可以极大地缓解内存瓶颈问题.
大多数的计算机拥有如下图所示的内存层级架构:
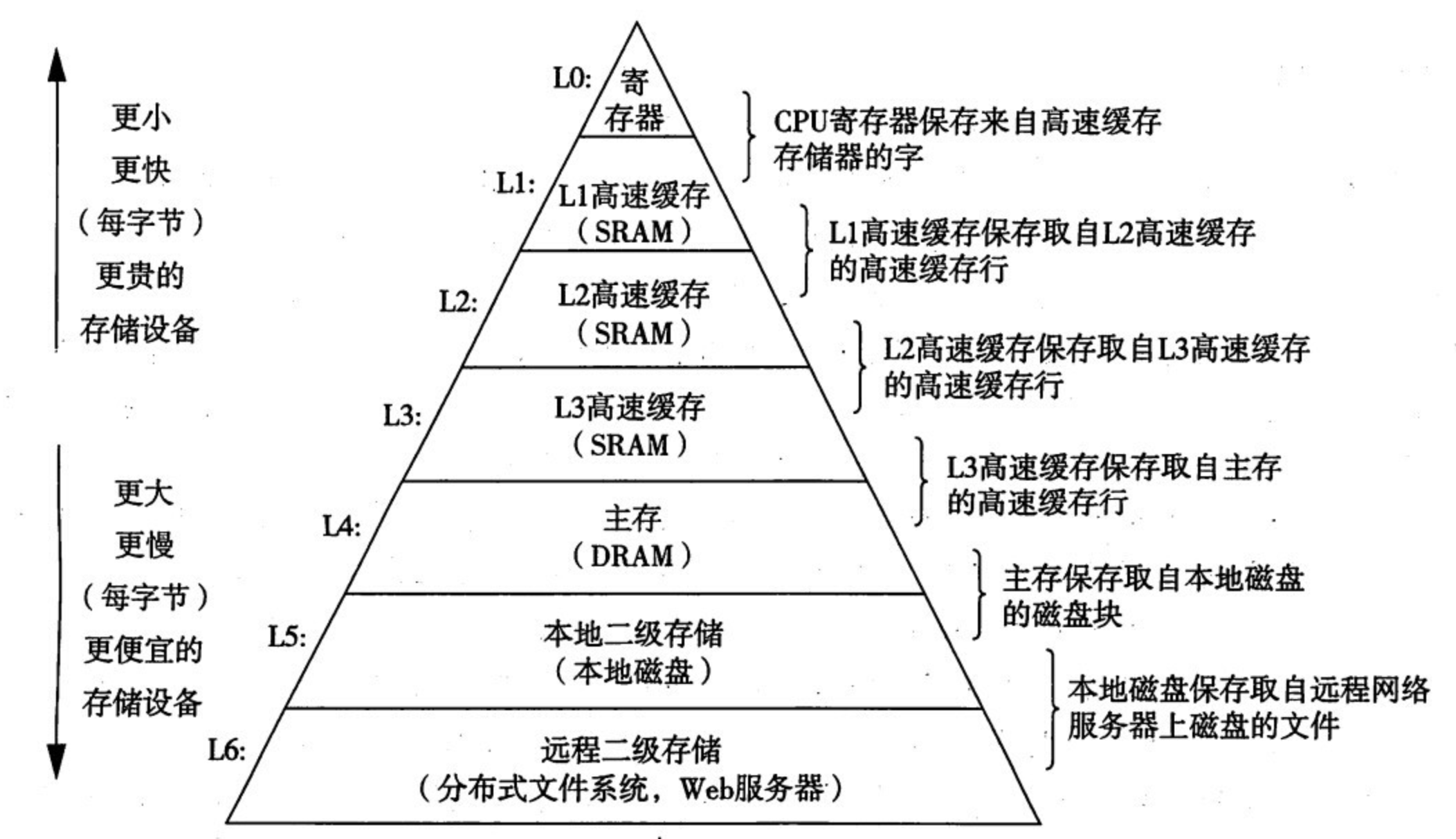
3. 寄存器池
现代处理器中一般都内置了数十个寄存器, 它们共同组成了所谓的 寄存器池 (Memory Bank). 这些寄存器用于存储程序运行所需的操作符和程序运行的 (中间) 结果.
寄存器的寻址方式和缓存, 主存等都是不同的, 但我们还是将其视为内存层级架构的最顶端 L0. 需要注意的是, 寄存器的使用和释放完全是由汇编语言的编译器或程序设计者完成的, 而不是一个完全自动的过程. 关于这一点, 我们可以在 COMP15111 的相关章节中详细了解.
4. 缓存
在内存层级架构中, 位于寄存器之下的即为缓存. 通过将被执行程序本身与其所需要的数据在执行时合理分配至不同性能的存储介质中, 我们可以在付出相对低得多的代价的前提下获得足够良好的性能表现, 这也是缓存的存在意义. 基于时间局部性和空间局部性, 我们可以使用缓存进行这样的优化:
简单来说, 局部性指程序倾向于引用临近于其余最近引用过的数据的数据项, 抑或是最近引用过的数据本身. 这意味着, 被引用过一次的存储器位置的内容在未来可能还会被多次引用; 若一个存储器位置的内容被引用了, 其附近的位置很可能也会被引用, 这也就是所谓的 时间局部性 (
Temporal Locality) 和 空间局部性 (Spatical Locality). 利用这一特点, 通过将最常被引用的数据存储在容量更小但速度更快的存储器中, 就可以大幅降低数据的读写速度, 从而让程序运行得更快.
在处理器执行某条指令或处理某个数据时, 它会在访问主存之前检查所需要的信息是否已经被存储在缓存中. 如果情况的确如此, 处理器就能以快得多的速度从缓存中获取所需的信息; 而如果并不是这样的话, 处理器将会把它所需要的信息和与之相关的一些信息 (基于空间局部性, 处理器会一并抓取后面几个内存地址中的信息), 并将它们存入缓存之中.
由于缓存在提升计算机性能方面有着巨大的作用, 现代处理器都会为内建的缓存再配置缓存 (“缓存的缓存”) , 这也形成了所谓的 缓存层级. 一般而言, 一级缓存被内建在处理器核心中, 二级缓存和三级缓存则被设计在处理器晶体内, 但相对远离核心的位置.
处理器向缓存中存储的信息不是一定会被使用的. 通过计算 缓存命中率 (Cache Hit Rate), 可以评价缓存利用程度的高低. 其计算公式如下:
5. SRAM, DRAM
SRAM (静态随机存储器) 是由锁存器 - 寄存器一步步搭建而来的, 其逻辑电路和处理器中所使用的一致, 因此具有和处理器的处理速度所相近的数据读写速度. 合理的使用方法是嵌入处理器中, 作为高速缓存. 但其电路面积更大, 且成本更高, 因此不适用于构建大容量存储设备.
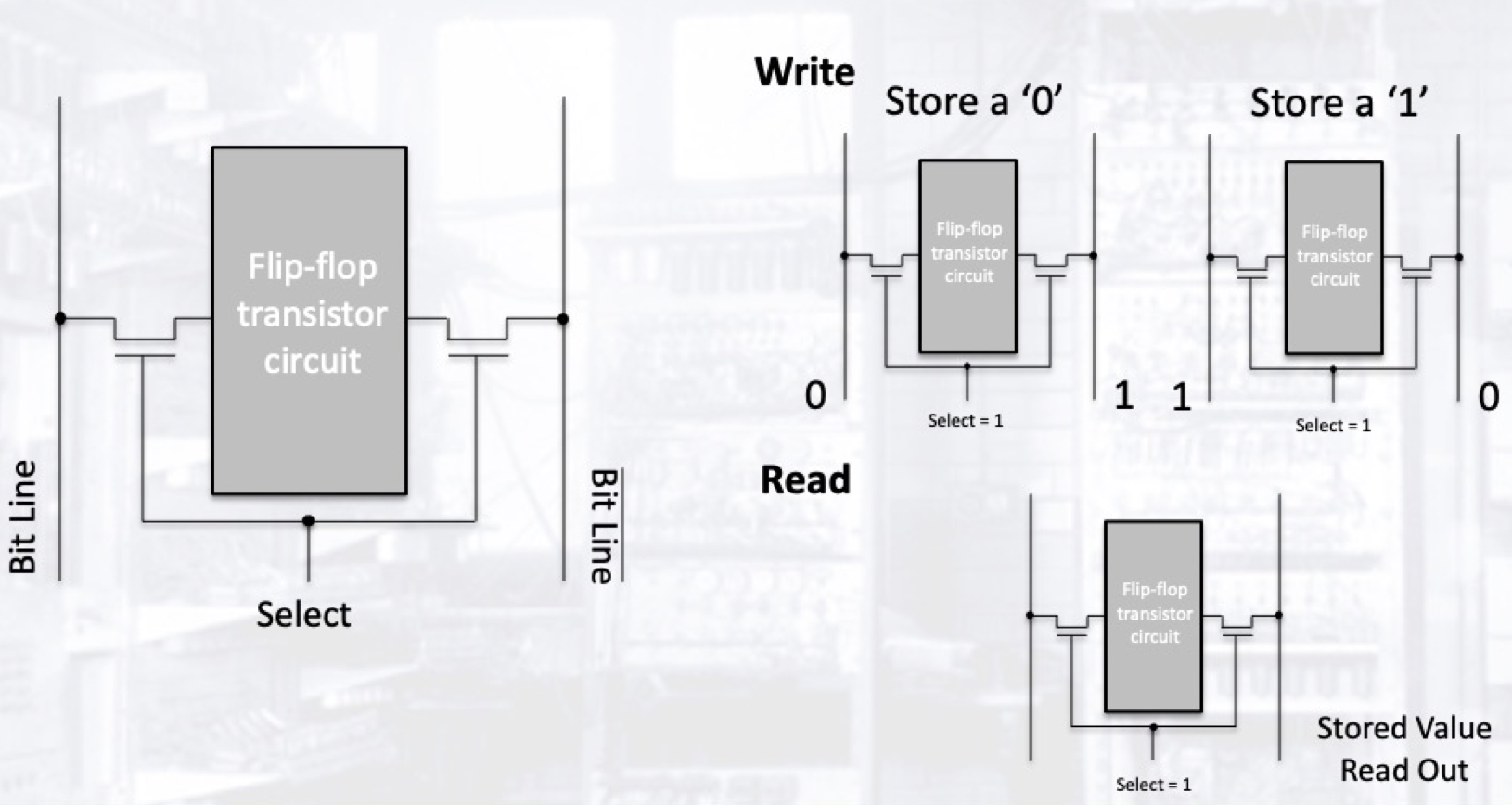
DRAM (动态随机存储器) 的核心是电容, 主控通过读取电容两端的电位值判断这个位所存储的是 $1$ 还是 $0$, 对存储器每一个位的读写都需要电容充放电, 因此虽然构成动态随机存储器的最小单元构造, 简单电路面积小, 但其读写速度远不如静态随机存储器.
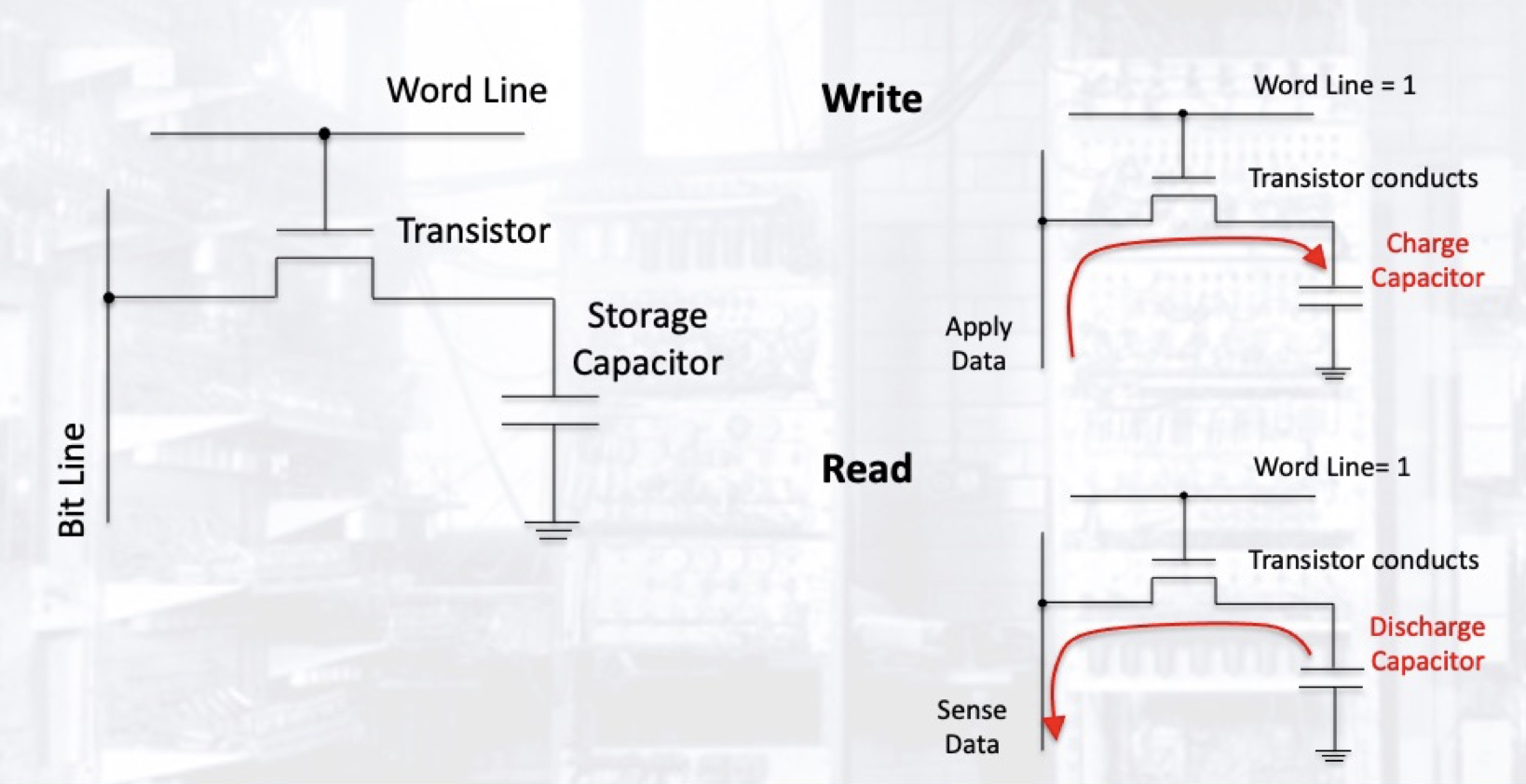
对 DRAM 的读取和写入流程如下:
DRAM写入 拉高Word Line, 闭合晶体管将存储电容器连接到Bit Line上. 若需要向该内存单元写入1的话, 就需要拉高Bit Line, 对电容器充电.DRAM读取 拉高Word Line, 闭合晶体管将存储电容器连接到Bit Line上, 并使用信号放大器检测Bit Line中是否有电流流动. 若有的话说明该单元中所存储的二进制位是 $1$, 否则是 $0$.
