Ch6 线性数据结构和位运算
Motivation:
- 使用合适的寻址模式访问线性数据结构
- 类
C语言的字符串 - 位运算和旋转
- 数组
1. 字符串和寻址模式
1.1 字符串
首先, 简介 Python 型字符串和 C 型字符串.
Python 型字符串中包含字符和一些额外信息, 如字符串长度, 字符串哈希值等.
C 型字符串包含字符, 每个字符长为一个字节 ($8$ 位), 并且最后以 ** 数字 $0$** 结尾. (注意: 不是字符 $’0’$!)
对于字符串, 我们有一系列的基本操作:
-
String.length计算某个字符串的长度:
For Python:
1
len = len(message)
For C:
1 2 3
len = 0; for (i = 0; len[i] != 0; i++); len = i;
For ARM Assembly (NOT Optimised):
1 2 3 4 5 6 7 8
ADRL R1, message MOV R2, #0 ; R2 used as the loop counter i again LDRB R0, [R1,R2] ; Register offset addressing ADD R2, R2, #1 CMP R0, #0 BNE again SUB R2, R2, #1 ; Why? Can this be avoided? STR R2, lengthFor ARM Assembly (Optimized):
1 2 3 4 5 6 7
ADRL R1, message MOV R2, #0 ; R2 = i again LDRB R0, [R1, R2] ; Register offset CMP R0, #0 ADDNE R2, R2, #1 BNE again STR R2, lengthFor ARM Assembly (Optimized for register use)
1 2 3 4 5 6 7 8 9 10
; Use Post-Indexed and save a register ADDRL R1, message ; Pointer to a char again LDRB R0, [R1], #1 ; Post Increment CMP R0, #0 ; Look for 0 BNE again ADRL R0, message SUB R0, R1, R0 SUB R0, R0, #1 STR R0, length ; Saved a register, but less concise or readable...
-
String.indexOf
在给定字符串中寻找给定字符第一次出现的位置:For Python:
1
msg.find(‘e’)
For ARM Assembly:
1 2 3 4 5 6 7 8
ADRL R1, message again LDRB R0, [R1], #1 CMP R0, #’e’ ;look for ’e’ instead of 0 BNE again ADRL R0, message SUB R0, R1, R0 SUB R0, R0, #1 STR R0, find
1.2 列表
我们以颜色表为例介绍列表:
显示设备可以输出大量不同的颜色. 广泛普及的显示屏的色彩输出范围至少都是数百万种颜色以上. 对于采用了位映射模式 (Bit-Mapped) 的显示设备而言, 它的每一个像素都可以显示一种不同的颜色.
考虑一个由三原色组成的像素点. 对于这样的一个像素点, 它的三原色输出强度均可被分别控制 (如: 每种颜色的强度可分为 256 级), 因而表示这样的一个像素点需要一个字节, 也就是八个位的存储空间.
用于查表的 ARM 代码:

在内存中, 指令和数据是这样存储的:
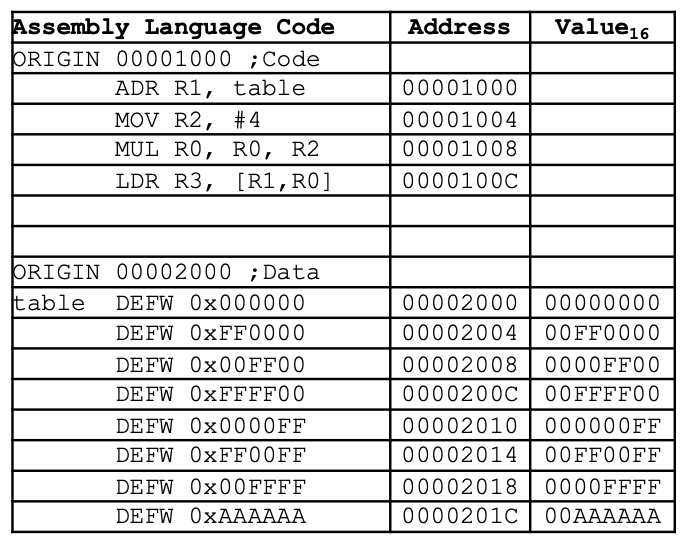
需要注意的是: 由于在该程序中我们使用 DEFB 定义变量, 为该变量分配的存储空间固定为 32 位 , 也就是 $4$ 个字节, 转换为 $16$ 位无符号整数后, 它的位数就是 $8$ ($2^{32} = 4 * (16)^2$). 而对于三通道的颜色表示法, 每一个通道的表示需要占用长为 $2$ 的十六进制位, 因此不管是什么颜色, 表示为十六进制无符号整数都是 0x00??????. 而众所周知, ARM 架构采用小端序, 因此在该表中, 所有的数据化为 16 进制无符号整数后, 其最高两位均空置为 0.
2. 位运算
位运算是对以二进制形式, 存储在计算机内存中的整数的二进制位进行的操作. 位运算通过对内存数据直接进行操作, 而无需转换为十进制后再运算, 因此运算速度极快. 通过使用合适的位运算, 我们可以对程序进行有效的优化.
2.1 位运算 - 逻辑运算
-
and按位与运算
运算规则和逻辑与运算相同, 用于二进制取位操作:
[例] 对一个二进制整数and 1的结果就是取该二进制整数的最末位. 所有的二进制奇数最低位均为 $1$, 而二进制偶数的最低位均为 $0$. 通过取某个二进制整数的最低位, 我们可以立即判断该数字的奇偶性.[例]
1 2 3
; Rn = 0b11001100, Op2=0b00001111 AND Rd, Rn, Op2 ; Rd = 0b00001100 ; clear all bits except those set in Op2
-
or按位或运算
运算规则和逻辑或运算相同.
[例]or运算通常用于对二进制整数的特定位进行无条件赋值. 如, 对一个二进制整数or 1的结果即为将其末位强行变为 $1$. 利用这一原理, 我们可以使用or运算, 通过对其和 $1$ 执行一次or运算后再减去 $1$, 即可将一个二进制整数变为最接近它的偶数.[例]
1 2 3 4 5
; Rn = 0b11001100, Op2=0b00001111 ORR Rd, Rn, Op2 ; Rd = 0b11001111 BIC Rd, Rn, Op2 ; Rd = 0b11000000 ; Set those bits that are set in Op2: any bit in Op2 that is 1, is set to ` in Rd ; Or CLEAR those bits that are set in Op2
-
not按位非运算
运算规则和逻辑非运算相同. 由于其定义即为将被操作数的每个位全部取反, 因此在进行按位非运算时需要注意被操作数是否为含符号整数. 若被执行数为一个无符号二进制整数, 则得到的结果即为该数和该类型上界的差. xor按位异或运算
运算规则和逻辑异或运算相同.
[例] 按位异或运算常用于对二进制整数的特定位进行取反操作. 并且, 取反运算与其本身互为逆运算, 亦即以任何一个二进制整数和另一个整数作为操作符, 连续执行两次异或运算的结果为其本身. 因此, 异或运算可用于简单的加密:1 2 3
114514 ^ 1919810 = 1897488 1897488 ^ 114514 = 1919810 1897488 ^ 1919810 = 114514
此外, 我们还可以使用异或运算进行变量的交换:
1 2 3 4
def swap(x, y) x = x ^ y y = x ^ y x = x ^ y-
LSL逻辑左移位运算
该运算由两个操作符组成:a LSL b即为: 将二进制整数 $a$ 左移 $b$ 位. 我们常用逻辑左移代替涉及 $2^n$ 的乘法运算.
[例]11011111101010010 (bin) = 114514 (dec),114514 LSL 2 = 458056, 亦即:a LSL b = a * 2^b. LSR逻辑右移位运算
和逻辑左移位运算相似, 逻辑右移位运算表示将二进制整数向右移位, 相当于将二进制整数除以 $2$ 的幂, 常用于代替特定的除法运算.
2.2 快速无符号二进制整数乘法 / 除法
见 “逻辑左移位运算” 和 “逻辑右移位运算”.
2.3 旋转操作
旋转操作就是循环移位运算.
2.4 ARM 移位指令
| 助记符 | 实际含义 | 行为 |
|---|---|---|
LSL #n |
逻辑左移 $n$ 位 | 将有符号或无符号二进制整数乘以 $2^n$ |
LSR #n |
逻辑右移 $n$ 位 | 将无符号二进制整数除以 $2^n$ |
ROR #n |
右旋转 $n$ 位 | 旋转位: lsb $\rightarrow$ Carry |
RRX #n |
右旋转并扩展 $n$ 位 | 围绕 Carry 位旋转位 |
2.5 逻辑运算
ARM 汇编语言中的布尔逻辑运算的定义, 运算类型和运算优先级与 Python 一致. 我们需要使用八个布尔值才能表示一个字, 但在涉及一些特殊的运算操作, 如从这个字中取出某一个特定位时, 如果这个字是用布尔值表示的, 那么我们只需要将其和一个特定的 $8$ 位无符号整数做与运算即可得知这个位上是 $1$ 还是 $0$. (此处不做解释, 自己思考一下应该如何实现)
通常, 我们认为 $1$ 为真值, 而 $0$ 恰好相反. 而在 C 语言中, 一切非零值均为真.
2.6 ARM 位运算
ARM 架构中的逻辑运算或布尔运算是以位运算的形式实现的:
1
2
3
4
5
; assume R1 = 0b11001100 R2 = 0b00001111
AND R0, R1, R2 ;R0 = 0b00001100 (AND)
ORR R0, R1, R2 ;R0 = 0b11001111 (OR)
EOR R0, R1, R2 ;R0 = 0b11000011 (XOR)
MVN R0, R2 ;R0 = 0b11110000 (NOT) invert R2, store to R0
注意:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
; 1.
; notice that although the 8-digit num has 0s on other higher bits, it is still considered as an 8-bit num instead of a 1-bit num!!
!00000001 == 11111110 != 0
; 2.
; assume we want to describe a formula:
; b4 = b1 & b2 | !b3
; take care that we must follow the operator order:
LDRB R0, b1
LDRB R1, b2
AND R0, R0, R1 ;do b1&b2 first
LDRB R1, b3
EOR R1, R1, #1 ;b3^1 = !b3
;for better performance, we wisely use decimal arithmetic quirks here
ORR R0, R0, R1 ;b1&b2 | !b3
STRB R0, b4 ;store the final result
ARM 架构提供了对每一个位执行 无条件赋值, 清除 (亦即将其值无条件赋值为 $0$), 和测试其值的方法.
对位执行无条件赋值和清除的例子我们已经在本文的 2.1 节相关例子中了解到了. 下面解释一下 “测试”:
1
2
3
4
; Rn = 0b11001100, Op2=0b00001111
TST Rn, Op2
; TST == 'Test': run Rn AND Op2, sets th flags, but discard the result.
; Op2 can be a reg, immediate value, shifted value, rotated value, etc.
此外, 由于某个数字的每一个位都可以被映射为某种状态的指示变量, 我们也可以通过对特定的变量的特定位执行逻辑运算, 间接地控制显示, 输出指令甚至操控硬件. 下面以一个简单的数显模块为例:

进一步假设, 通过在地址 display 中存储一个字, 我们就能控制这个数显设备的开闭和显示的内容:
1
2
3
4
5
6
7
8
ADR R1, segments
LDRB R2, [R1, R0]
STRB R2, display
segments: 00111111 ; display 0
00000110 ; disply 1
01011011 ; display 2
......
但在此处我们可知, 若 R0 的值过大的话, 以它作为寄存器间接寻址的偏移量可能会导致 R2 中存储的值实际上超出了列表 segments的范围, 发生越界导致数码显示效果不可预知. 为了部分解决这一问题, 我们需要在将 R0 作为偏移量之前, 将其最低四位以外的全部二进制位强制归零:
1
AND R2, R0, #0b1111
2.6 短路特性
在对布尔表达式进行检查时, 我们可以利用逻辑运算的短路特性简化对表达式的判断逻辑. 以下面的例子为例:
1
2
3
4
5
6
7
8
9
10
11
b = (x<y and y<z) or (x>z)
we can rewrite to test x<y first:
if (x<y): b = (True and y<z) or (x>z) # if x<y True
else: b = (False and y<z) or (x>z) # if x<y False
equivalent to:
if (x<y): b = (y<z) or (x>z)
else: b = x>z
简单的概括短路特性的利用方法, 就是:
- 与运算具有最直接的短路特性: 只要其中一个条件为假, 则整个表达式必为假:
- 或运算同样具有短路特性: 只要其中一个条件为真, 则整个表达式就为真.
因此, 在将逻辑表达式转换为条件判断语句时, 我们常常可以先判断与运算中的某个条件, 随后再对或运算进行判断; 这样的话可以实现条件判断逻辑的简化, 无需对逻辑运算中的每一个条件都进行一次分别的判断.
参考:
位运算简介及实用技巧 (一) : 基础篇
人造奇迹——二进制位运算的运用
3. 数组
数组是一种广泛应用于科学计算, 深度学习等领域的数据结构. 下面我们对数组进行介绍.
3.1 数组的定义, 访问和存储
我们首先回顾以下数组数据结构在高级程序设计语言中的定义和访问. 数组中数据的存储方式是连续的, 具有局部性的特点, 可以通过循环或多层循环嵌套 (针对高维数组) 的方式对其元素进行依序访问.
在内存中, 一维数组的元素被连续存储, 每一个整数数组的元素均占用了 $4$ 个字 (即 $32$ 字节) 的空间. 要访问这样的一维数组, 我们只需要知道数组头元素的内存地址和要访问的数组元素在数组中的编号 (Index), 就可以计算出指向该元素的指针, 从而对其访问.
[例]
数组头元素的内存地址为 1FAB4000, 我们要访问该一维整数数组中的第 $i$ 个元素. 根据整数数组数据的存储方式, 我们计算出的元素指针为 1FAB400 + 4*i.
在 ARM 汇编中, 定义数组的方法如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
; Array of student heights
; Note: single byte per student: +ve integer heights <256cm
; Note: the program does not have a zeroth student
; so pad the array
HEIGHTS DEFB 0,150,160,165,155,150,170,175,180,155,160
; Set up base address and index
MOV R2, #10 ;Index set to student number 10
ADR R4, HEIGHTS ;Make R4 the pointer to the array
; Access element 10 o the array using indexed addressing
MOV R2, #10 ;Set the current student num to 10
LOOP LDRB R1, [R4, R2] ;Height is at base address + I
在高级程序设计语言中, 对一维数组的连续访问伪代码如下:
1
2
for i in range(1, 10):
print(a[i])
而在 ARM 汇编中, 上述代码被直接翻译为:
1
LDRB R1, [R4], #1 ;fetch [R4], then R4 += 1
但这样的方法会导致指向数组头的初始指针的指向发生变化. 因此, 我们往往采用基指针 + 偏移量的方式, 结合位运算实现数组的高效访问:
1
2
3
4
5
6
LDRB R1, [R4, R2] ;for array of bytes
; and...
LDR R1, [R4, R2, LSL #2] ;for array of 4-byte words
; do logical shift left by 2, multiply the difference by 4
数组中既可以直接存储数字等数据, 也可以存储指向其他内存位置的指针:
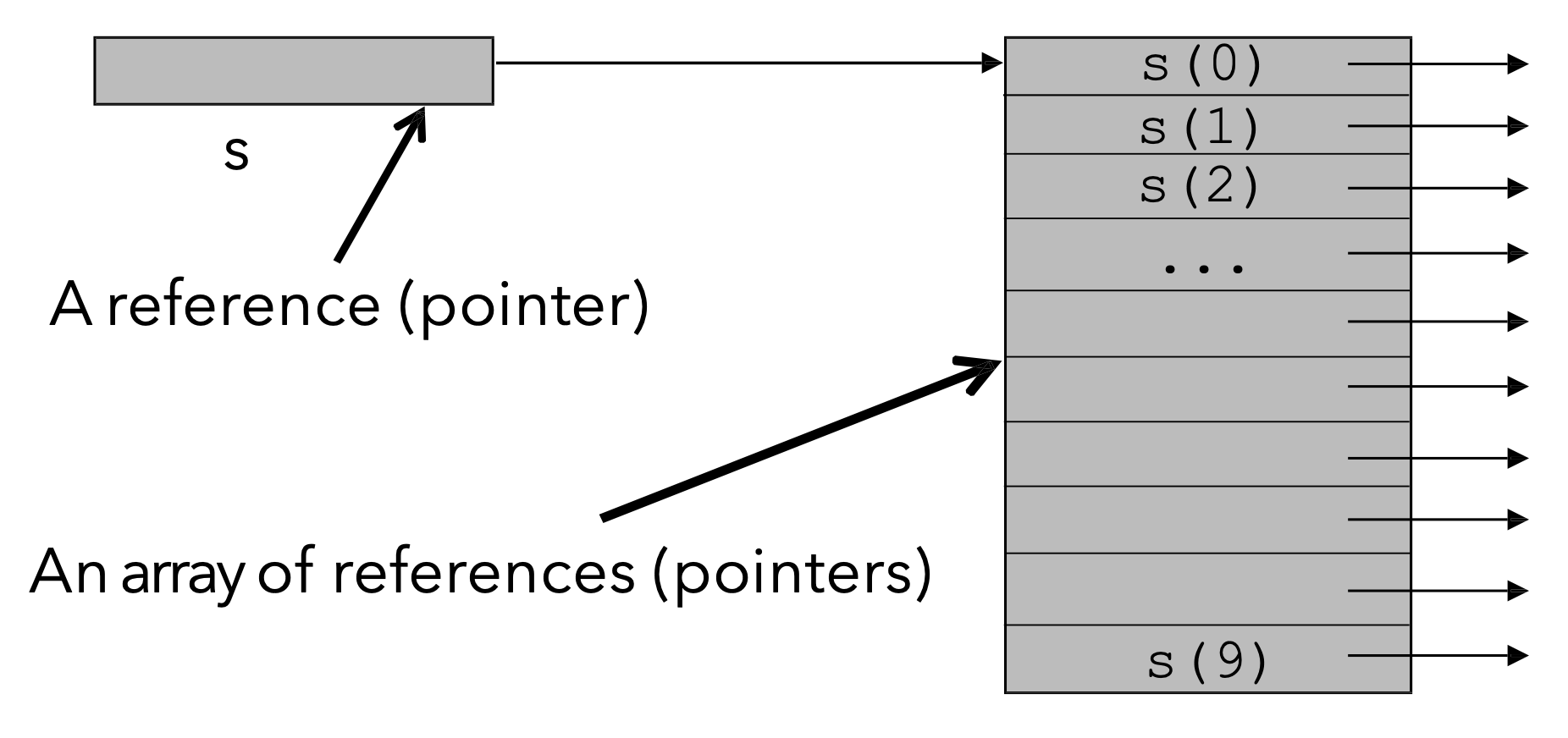
以一个存储字符串的数组为例:
1
s[2] = "abcd"
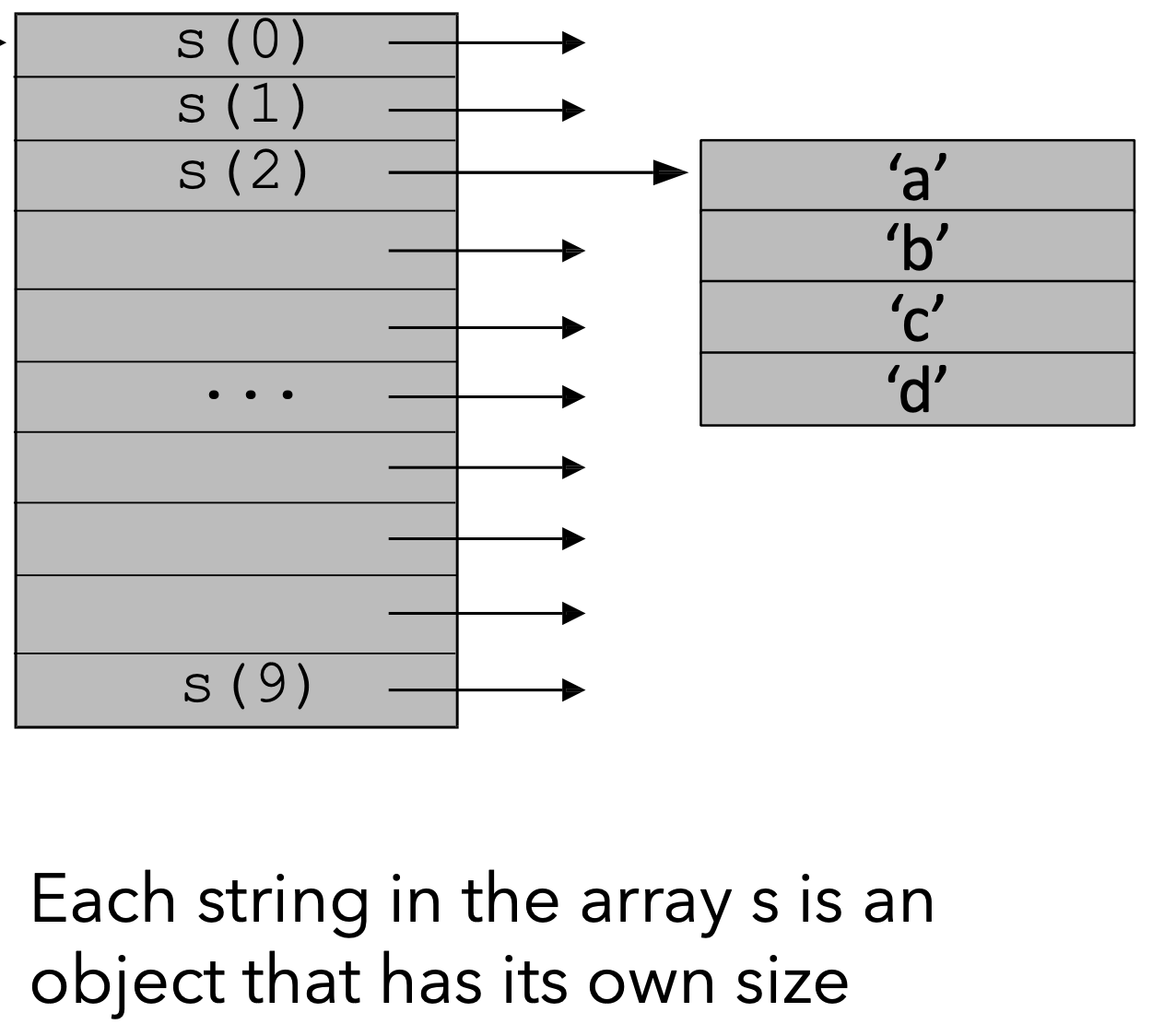
数组 s 中的数据存储结构如下图所示:
3.2 高维数组
下面考虑高维数组:
1
m = [[0, 1, 2, 3], [4, 5, 6, 7]]
其数据结构可被视为二元矩阵, 每一个元素均有两个对应的标识符指示它在矩阵中的行数和列数.
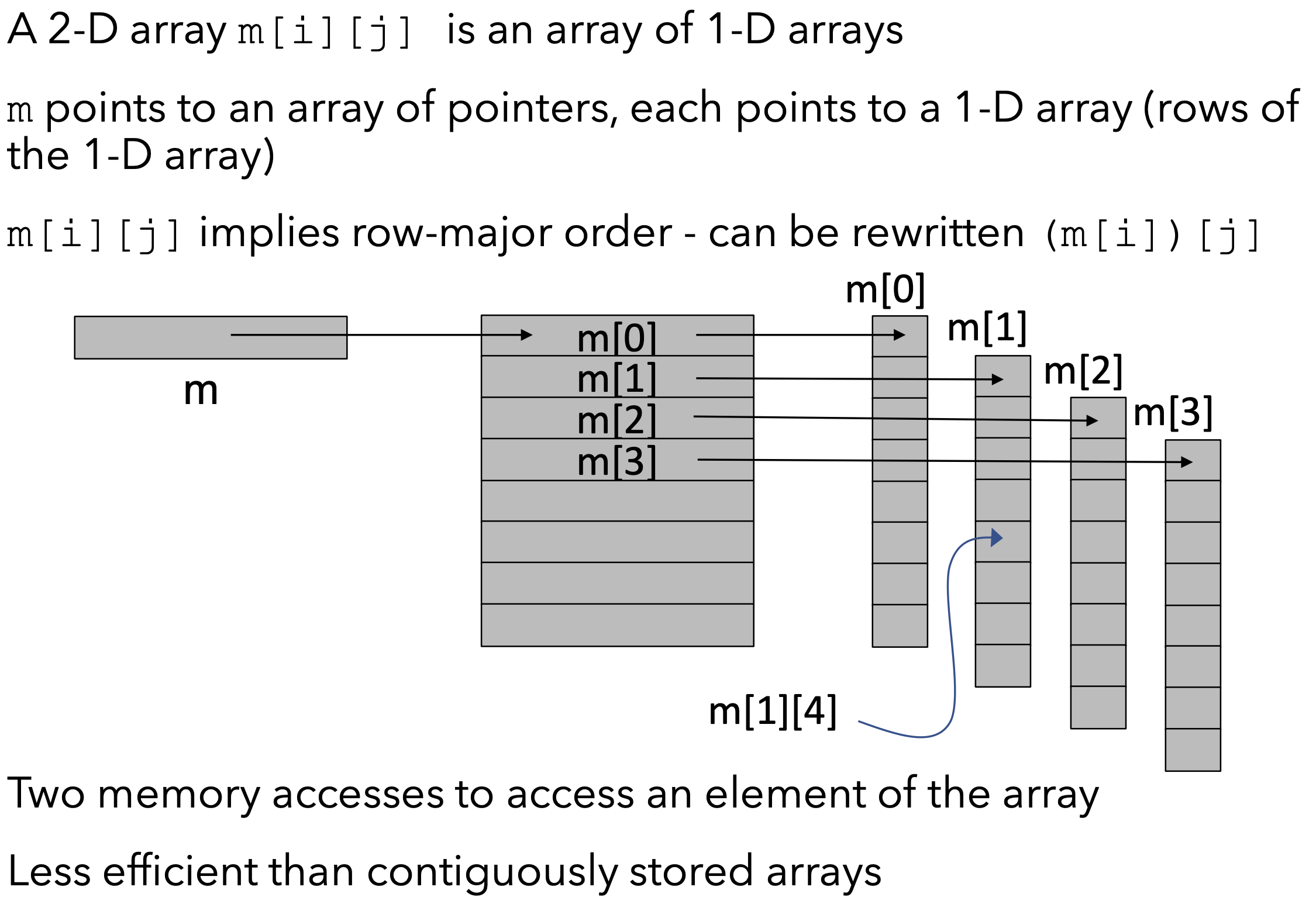
一种常见的, 存储高维数组的方法时将其以行为单位, 将其视为多个长度相同的一维数组连续存储. 在确定行数和列数, 并给定了高维数组的起始指针的情况下, 我们可以很轻松地实现对全数组的任意访问.
下面我们简介一种基于面向对象思想的数组存储方法, 该方法用于 Python 中的数组存储:
该方法将二维数组定义为一列由指针构成的一维数组, 而一维数组中的每一个指针均指向一整行. 要将二维数组存储扩展到三位甚至更高维, 我们只需要再嵌套一层层级更高的指针数组即可. 如存储三位数组, 我们就需要两层指针数组和一层数据数组: 最高层指针数组存储全部的二维数组, 而每一个二维数组又被拆分为一层指针数组和一层数据数组.
这样的存储方法非常符合逻辑, 但其存储复杂性会随着存储维度的增加而递增, 其访问速度也会随之下降.
3.3 数组/内存边界检测
为了避免异常发生, 我们必须确保程序在执行时不会对超出实际可访问范围的内存地址进行访问, 或在访问数组时尝试读取超出数组边界的值.
我们首先讨论数组边界检测. 其基本原理是: 我们预先存储数组的边界值, 并且在每一次数组访问前都检测访问目标值是否超出边界:
1
2
3
4
5
6
7
; assume we have the code b = a[x * x]
; R2 is the pointer which contains the base address
; R1 is used as the index, R0 contains x
MUL R1, R0, R0 ; x * x
CMP R1, #N; ; compare R1 and bound N
BGE error ; handle exception if index > N
LDR R3, [R2, R1, LSL #2] ; 32 bit
该方法要求对于每一个定义的数组, 我们都要相应存储它的大小用以检测是否发生了越边界访问. 不过, 实际上另一种可能的异常是出现了低于下边界的访问, 这也是越边界访问异常, 因此我们不仅要对上界, 还要对下界进行检测.
无论如何, 对数组访问进行边界检测在每次访问时都会被执行, 边界检测需要额外的代码和寄存器/内存, 消耗处理器时间和硬件资源. 因此, 在完全确定我们编写的汇编程序不会对数组进行越界访问的情况下, 我们可以要求编译器忽略对数组的边界检测实现程序的 “优化”.
下面我们对内存边界检测进行简要讨论.
操作系统会对可支配的内存进行管理, 用户可访问的内存空间会受到操作系统内建的内存管理系统的分配和限制. 此外, 数据存储和程序存储可能也会被分离, 但是这样的机制无法阻止用户程序访问属于其他用户的内存空间, 因此仍需进行内存边界检测.
