Ch3 RTL 设计和有限状态机

在本章中, 我们将简介寄存器传输级别逻辑设计, 以及有限状态机的相关概念:

1. 更为深入地了解顺序系统的设计
2. 介绍寄存器传输级别设计
3. 介绍有限状态机, 以及设计有限状态机的两种工具
4. 更为深入地了解数据路径与其控制

1. 顺序系统设计: 寄存器传输级别 RTL

大部分的数字电路系统都是顺序的而非组合的, 由触发器和逻辑门电路组合而成. 更复杂的电路一般又由多个模块通过线路相连接而成, 每一个模组又包含了寄存器. 因此, 寄存器传输级别 RTL 既可以提供足够合理的抽象程度, 又可以提供足够的门级电路控制, 因而成为现今电路设计的主流.

1.1 定义

我们可以这样理解 RTL:
Register 指一系列由触发器组合而成的, 可以暂时地存储长为数个位 (bits) 的信息的电路. 它们所存储的信息可以是:

• 某个状态值
• 某个数值
• 某条指令
• 某个颜色

Transfer 指代的是我们要将数据在寄存器之间专一的需求. 比如:

• 进行某种运算
• 在某些情况下对操作进行预测

当一个数字电路系统满足以下条件时, 一般将其以寄存器传输级别表示:

• 在系统中有数个寄存器
• 运算和操作的执行涉及了存储在寄存器中的数据
• 系统中的操作序列受到控制

注:

1. 我们可以使用在 Ch1 中介绍的方法构造可被实现为组合逻辑块的简易逻辑表达式. 但是, 当需要实现的功能变得复杂时, 我们必须考虑逻辑表达式的化简问题.
   
   首先, 我们可以简化逻辑表达式考虑的情形数量. 在一些情形中, 我们可以将某些特定输入视为无效值, 但我们往往不能将输出信号设为任意值, 因为这可能会导致意想不到的不良结果. 因此, 即使我们认定某一些输入是无关紧要的, 我们也应该为其分配一个特定的输出值 (一般我们会选择低电平输出或高阻输出).
   
   此外, 我们可以使用布尔代数和卡诺图对逻辑表达式进行进一步的化简. 即使我们不去专门地优化逻辑表达式, CAD 工具也会使用内建的算法对其进行优化. 在本课程中, 我们就将逻辑简化过程留给编译器好了.

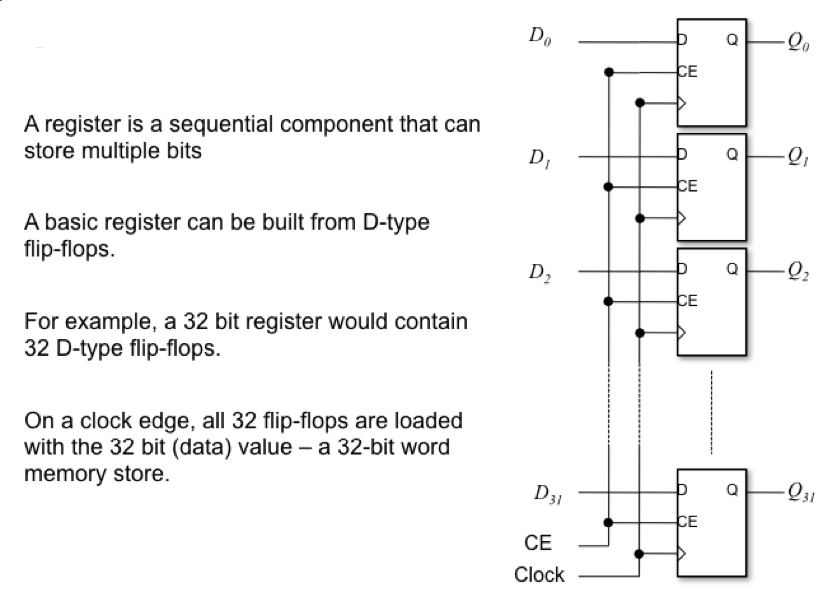
1. 寄存器是一种由一组触发器构成, 用于保存二进制数据的存储设备. 每一个触发器只能存储一个位. 因此, 若我们要存储一个长为 $32$ 位的字, 就需要 $32$ 个触发器.
   
   一个典型的寄存器由多个触发器共同构成. 在寄存器中, 每个触发器都有独立的输入和输出线路, 但所有的触发器的时钟输入都是相同的. 也就是说, 触发器的同步是被强制执行的, 在时钟使能时, 所有的位都会被同时切换.
   
   通常我们在设计中使用符号抽象化表示寄存器 (如下图). 由于对同一电路中的所有寄存器而言, 时钟都是被共用的, 因此它往往会被省略不写.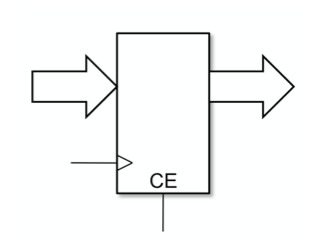

   

1.2 RTL 设计流程

标准设计流程分为两步: 定义输入和相应的输出 (也就是确定电路的行为), 并基于定义将行为转化为实际的电路设计.

1.3 数据路径与其控制

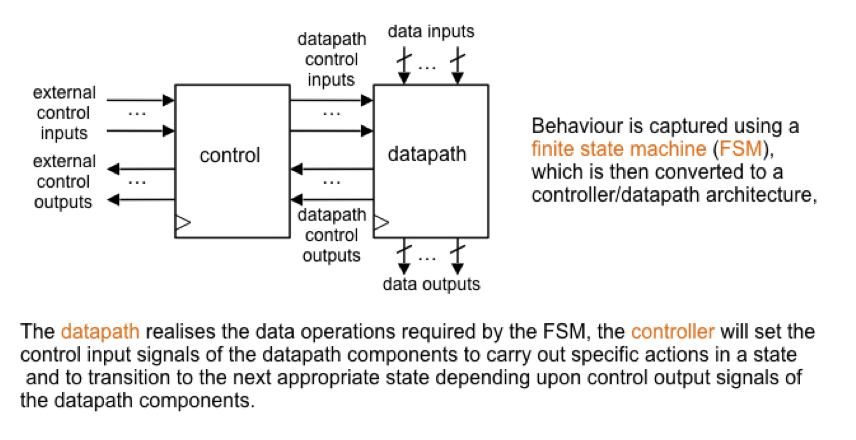
在 RTL 层级中, 数据流经寄存器和组合逻辑电路序列. 在这个序列中, 寄存器用于存储数据, 而组合逻辑电路对寄存器中存储的数据进行一些逻辑操作, 并将被操作后的数据在下一个时钟脉冲时载入另一个, 或同一个寄存器中, 进而进行下一步的处理. 因此, 我们可以将顺序系统视为一个由一系列的寄存器和组合逻辑电路块所构成的系统, 数据在每一个时钟脉冲处, 从一个寄存器/组合逻辑电路块流动到下一个寄存器/组合逻辑电路块中.

数据沿着特定的顺序流动, 这样的顺序即被称为数据路径. 对数据路径流向的管理由控制电路块负责. 它基于系统当前的状态, 将控制信号输入至数据路径, 从而控制数据如何沿路径流动.

使用这样的数据路径和控制方法, 我们可以设计出几乎任何的顺序系统. 对于一些不对数据进行处理的简单系统, 我们只需要一个控制块, 以基于当前状态和输入信号的状态, 从一种状态转移至另一种状态. 对系统当前状态的保存可以使用寄存器完成.

2. 有限状态机 FSM

基于 RTL 设计流程和 RTL 数据路径, 就立即引入了有限状态机的概念.

有限状态机, 就是由状态寄存器和组合逻辑电路构成，能够根据控制信号按照预先设定的状态进行状态转移的电路.

当我们研究设计组合电路时, 我们简单地采用布尔表达式, 并将其化简并转换为逻辑门电路. 但显然我们并不能使用布尔表达式描述顺序系统. 有限状态机是一种可以描述设计随时间变化的行为的方法, 它可以良好地表示顺序系统.
在状态机中，下一状态 由一组确定的规则决定，并受当前状态 以及 当前接受的输入 共同决定.
FSM 由一组状态组成, 这些状态代表系统可能处于的每种可能情况.
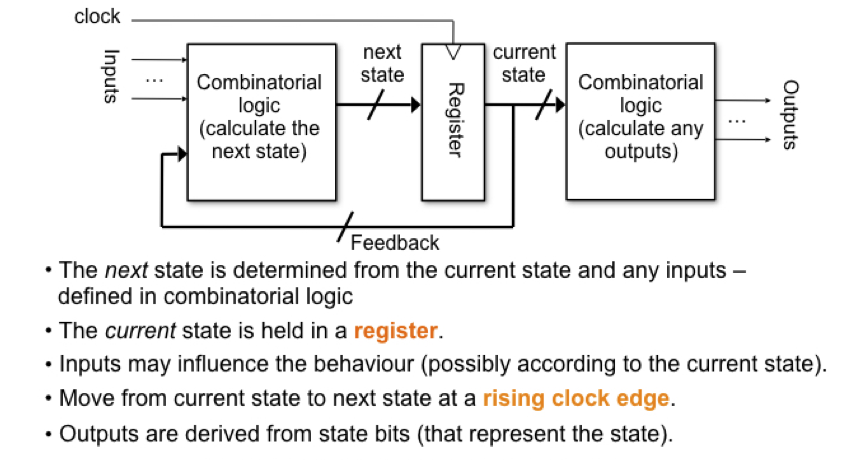
FSM能且只能在任何时间处于一种状态，这称为 当前状态. 下一状态 由 当前状态 和 FSM 的任何输入信号的状态确定。组合逻辑块（或称为下一状态逻辑块）确定下一个状态, FSM 将在下一个时钟脉冲时转移至该状态. 从当前状态到下一状态的转换（通常）发生在外部时钟的高电平上升沿上. FSM 根据确定这些状态之间过渡的各种条件，简单地在不同状态之间转移.
FSM 的当前状态以二进制码存储在寄存器中。下一状态（由下一状态逻辑块计算）在下一个时钟脉冲时被锁存到寄存器中，并成为控制器的当前状态。

有限状态机所涉及的状态一般数量繁多且关系复杂. 要设计有限状态机, 我们可以使用以下的两种方法.

2.1 状态转换图

状态转换图是一种以图像的形式, 直观体现状态间的先后顺序和状态转换条件的方法. 它虽然简单直观但效率低下, 不适于表示复杂状态, 一般不常用.

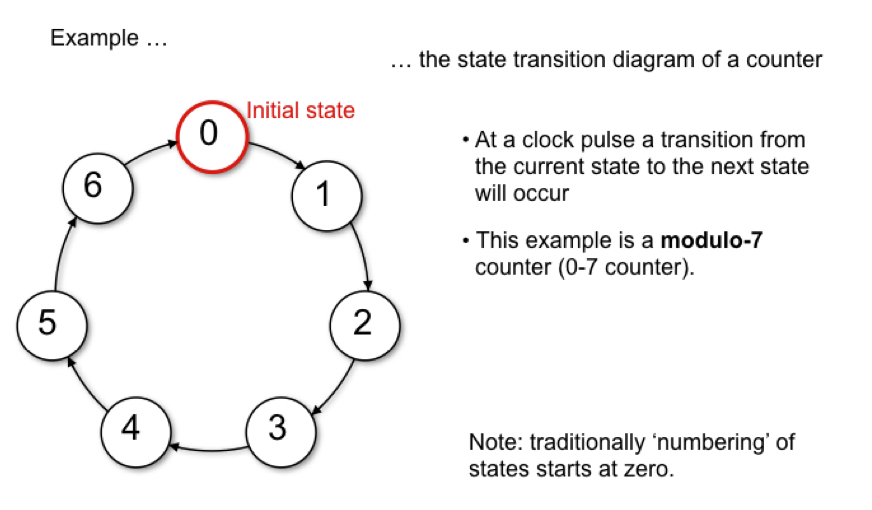
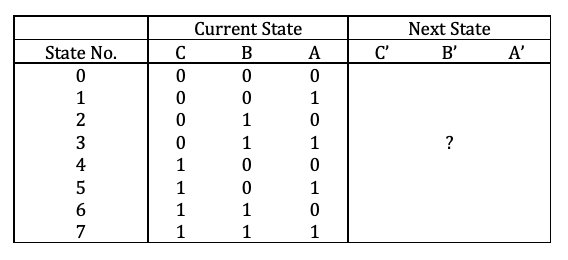
2.2 状态转换表

状态转换表是是表格形式的状态转换图，两者本质是相同的。状态转换表有两种形式，一种是使用现态和次态表达时钟脉冲到达前后的状态变化，这种方法不需要单独列出时钟脉冲；另一种是按照时间前后顺序依次将各个状态列出.

2.3 同步时序逻辑 (Synchronous Paradigm)

同步时许逻辑指表示状态的寄存器组的值只能在唯一确定的触发条件发生改变的逻辑.

只能由时钟的正跳变沿或者负跳变沿触发的状态机即为一例:

1
always@（posedge clk）

同步时序逻辑的优点：

1. 同步时序逻辑比异步时序逻辑稳定简单得多.
2. 在较复杂的系统中, 当信号沿着不同路径流动时, 组合逻辑电路可能因为它们到达输出端的先后时间差异而产生 “故障”, 若使用同步时序逻辑, 即可允许这些信号在时钟转换发生之前先后到达输出端, 从而避免故障.
3. 使用同步时序逻辑, 我们可以将来自不同模块的输出 “同步”.
4. 通过计算时钟周期数, 同步时序逻辑系统的时序可以被轻松预测.
5. 编译器更适合编译同步时序逻辑电路.

2.4 异步时序逻辑 (Asynchronous Paradigm)

异步时序逻辑指触发条件由多个控制因素组成, 且任何一个因素的跳变都可以引起触发的逻辑. 寄存器组的时钟输入端并不连接在同一个时钟信号上.

考虑用一个触发器的输出连接到另外一个触发器的时钟端去触发这个触发器, 这就是一例异步时序逻辑.

异步时序逻辑的缺点：

1. 因为异步时序逻辑的触发条件很随意，任何时刻都有可能发生, 因此难以预测这样的逻辑系统的时序.
2. 许多编译器都不支持异步时序逻辑的编译.
3. 异步时序很难控制由组合逻辑和延迟产生的 “信号竞争” (不同步).

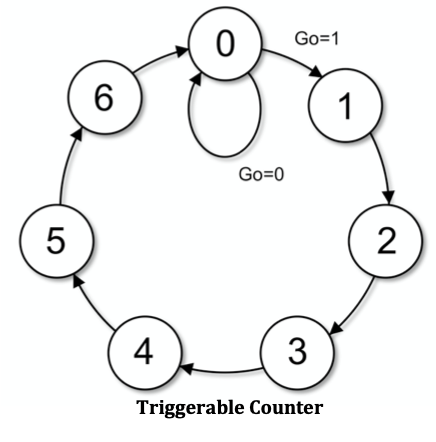
2.5 条件状态转换

有的有限状态机控制状态转换的条件不仅包括时钟脉冲, 还包括某个特定的外界输入值. 这就是条件状态输入转换.

需要注意的是, 外界输入不得和有限状态机状态寄存器的设定时间 (Set-up time) 与延迟时间 (Hold time) 相冲突. (具体细节在Ch1中被详细介绍), 这通常意味着外界输入需要和状态机的运行同步.

3. 有限状态机的 Verilog 实现

在 Verilog 中实现有限状态机是相当直观的:

1. 有限状态机应该被视为一个模组, 或嵌在一个模组中.
2. 这个模组应有一个时钟输入:

   1
    module FSM (input clock);
   

3. 由于状态变化总是在时钟上升沿上发生, 故需使用阻塞赋值:

   1
    always @ (posedge clk)
   

   随后, 我们将在 always 块内定义该有限状态机的行为.

下面, 以一个 “对 $7$ 取模的有限状态机” 为例:

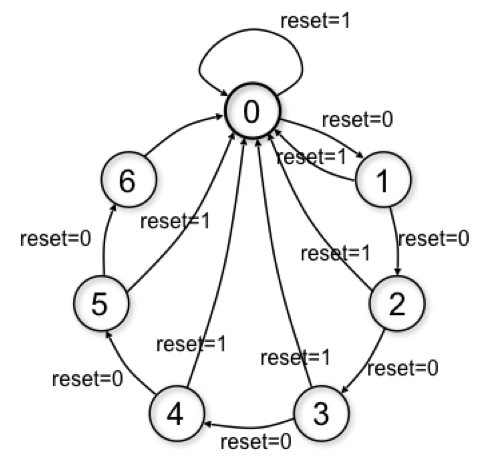
可见, 这是一个包含条件状态转换的有限状态机. 一种实现方式如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
always @ (posedge clk)
    if (reset == 1) 
        state <= 0;
    else
        case (state)
            0: state <= 1;
            1: state <= 2;
            2: state <= 3;
            3: state <= 4;
            4: state <= 5;
            5: state <= 6;
            6: state <= 0;
            default: state <= 0;
        endcase

3.1 有限状态机条件转换

在条件状态转换简单的情况下我们可以放心地使用 if 语句控制条件, 但当它变得复杂时, 再使用 if 就不能良好地定义 (例如: 倘若对每一个状态而言, 它们都有自己不同的状态转换条件, 此时又该如何用 if 语句定义?). 更一般地, 我们可以这样定义:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
module mod_7_count(input clk, reset, output reg [2:0] state);
    input  clk, reset;
    output [2:0] state;
    always @ (posedge clk)
        case (state)
            0: if (reset == 1) state <= 0; else state <= 1;
            1: if (reset == 1) state <= 0; else state <= 2;
            2: if (reset == 1) state <= 0; else state <= 3;
            3: if (reset == 1) state <= 0; else state <= 4;
            4: if (reset == 1) state <= 0; else state <= 5;
            5: if (reset == 1) state <= 0; else state <= 6;
            6: state <= 0;
        default: state <= 0; // Just in case! endcase
endmodule

3.2 有限状态机设计分区

在需要被定义的有限状态机更加复杂时, 我们就需要对状态机的设计进行 分区: 我们一般将复杂有限状态机的设计作如下划分:

• 输入逻辑: 根据当前状态和输入确定状态机的下一状态
• 状态逻辑: 执行状态变换
• 输出逻辑: 生成并确定输出信号的值

其逻辑结构和下图展示的抽象状态机类似:

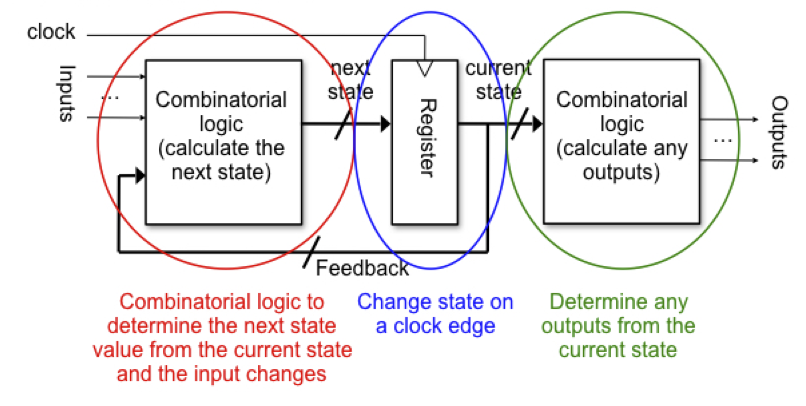
3.2.1 输入逻辑: 下一状态

输入逻辑根据当前状态和当前输入确定状态机的下一状态. 因此:

• 它可被 always 块表示
• 敏感度列表包含了可使状态发生变换的输入信号, 以及指示当前状态的信号
• 使用 case 语句列出所有可能的当前状态:

  1
  2
  3
  4
    case (current_state)
        0: next_state = 1;
        1: next_state = 2;
        ...
  

• 使用 if 语句确定受某个输入所确定的状态变换:

  1
  2
  3
  4
  5
  6
  7
    case (current_state)
        0:  if(wait == 1) 
                next_state = 0;
            else
                next_state = 1;
        1:  next_state = 2;
        ...
  

• 切记: 一定要设定 default 情形:

  1
  2
  3
  4
  5
  6
    case (current_state) 
        0:  next_state = 1;
        1:  next_state = 2;
        2:  next_state = 0;
        default:    next_state = 0; 
    endcase
  

3.2.2 状态逻辑: 执行变换

状态逻辑的功能是执行状态变换, 将状态变换到输入逻辑所生成的下一逻辑.

在时钟上升沿，状态机要变换到由输入逻辑所确定的下一逻辑. 我们可以在敏感度列表中添加时钟的上升沿来实现此过程:

1
always @ (posedge clock)

为了将下一状态赋值到当前状态, 我们使用非阻塞赋值:

1
current_state <= next_state;

要实现同步复位 (Synchronous Reset) 功能, 我们可以在 always 块中进行相应的定义.

3.2.3 输出逻辑: 进行输出

输出逻辑是组合的. 因此, 我们使用 assign 连续赋值语句.

3.2.4 数据流和控制

典型的数字系统可以被分为数据部分和控制部分.

和数据存储与处理相关的模块共同构成了数据路径, 而控制就是指控制数据路径的模块. 在数字系统中, 这两个部分相互作用. 控制模块会告知数据路径要执行的操作以及何时执行它们. 数据路径对控制模块的影响较小, 在一些设计中它们会返回控制模块行为的值.

以处理器取码, 译码和执行为例:

• 取码：输入地址，读取指令
• 译码：确定指令应执行的操作
• 执行：更改处理器的寄存器（或控制）状态 具体指令如何执行取决于所获取的指令. 在取码过程中, 通常会涉及一些控制序列，但这完全与取得的值 (指令) 无关.

对于不同的指令，译码过程可能会有所不同，但是操作类别少于 $2^{32}$，因此仍会有相当的通用性 (例如, 控制模块可能不在乎正在使用哪个寄存器).

执行可能会有 (极少数) 不同的行为。但是，控制器可以命令执行 ADD 指令，但不关心数据路径中添加了什么数值 (来自 $2^{64}$ 种不同可能的组合).

寄存器传输级别 RTL 是一种利用数据和控制分离的方法，以简化设计过程. RTL有效地忽略了数据的不同值或状态, 而将它们视为单独的变量. 因此, RTL 是比门级设计 ”更高级“ 的层次 “级别”.

当然，子系统不是完全无关的. 数据路径会提供解码指令, 因此会影响解码阶段的控制. 在少数情况下, 指令在执行期间也会产生影响. 以条件分支为例: BNE可以指定 “若不等于则执行分支”. 若指定的数据值非零, 则会发生跳转, 否则该指令将被忽略.

我们还可以进一步细分数据路径: 可以为每个指令处理阶段构建单独的单元. 这种方法在高性能处理器中很常见.

• Previous
  回溯算法
• Next
  Ch6 编译原理 线性数据结构和位运算