Ch1 逻辑门电路
在本章中, 我们将学习数字信号和基于二进制的数据表示法, 布尔代数逻辑和表达式 (具体的理论部分将在课程: COMP11120 计算机科学数学工具包中进一步阐释), 逻辑门电路, 二进制运算, 抽象和分级的设计思想, 时钟和顺序系统.
1. 数据表示法
由于在二进制中, 任何一个数码有且只有两种状态, 这与电路的开闭, 电位的高低天然契合, 因此现代计算机使用二进制对数据进行表示.
1.1 二进制整数的无符号表示法
无符号整数是只包括 $0$ 和正数的非负整数. 一般而言, 计算机都会定义一个称为 最大无符号整数 $2^n-1$, 而 $n$ 是计算机中, 分配用于表示无符号整数的二进制位数.
无符号整数存储法可以提升存储数据的效率: 由于无需存储整数符号, 因此所有分配的二进制位单元均可用于存储数字.
1.2 二进制整数的补码表示法
几乎所有的计算机系统均使用 二进制补码表示法 存储位于 $n$ 位存储单元中的有符号整数. 在该方法中, 无符号整数的有效存储范围 $0 - 2^{n}-1$ 被划分为两个大小相等的子范围, 分别用于存储 非负整数 和 负整数: $[-2^{n-1}, -1]$ 以及 $[0, 2^{n-1}-1]$.
在二进制补码表示法中, 最左位 (小端序下视为最高位) 作为符号位.
1.3 二进制实数的浮点表示法
实数是带有整数部分和小数部分的数字. 为了确保存储精度, 对于带有很大的整数部分或很小的小数部分的实数, 需要用 浮点表示法 来进行表示.
浮点表示法允许小数点的幅度, 从而增加了可存储的实数范围. 在浮点表示法中, 无论二进制还是十进制, 一个数字均由三个部分组成:
- 第一部分是 符号, 可正可负 ($0, 1$).
- 第二部分是表示小数点应该左右移动从而构成实际数字的 偏移量.
- 第三部分是小数点位置固定的 定点数.
2. 布尔表达式和真值表
逻辑运算包含二进制输入和二进制输出. 基本的布尔函数包括 AND, OR, NOT:

2.1 布尔代数简述和布尔表达式
见博文: 逻辑学探幽.
2.2 真值表
见博文: 逻辑学探幽.
3. 逻辑门电路和二进制运算
3.1 逻辑门电路
逻辑运算通过布尔代数进行化简, 运算和表示, 而在实际的电路中, 逻辑运算由 逻辑门电路 搭建而来. 逻辑门电路在电路图中的符号表示如下;
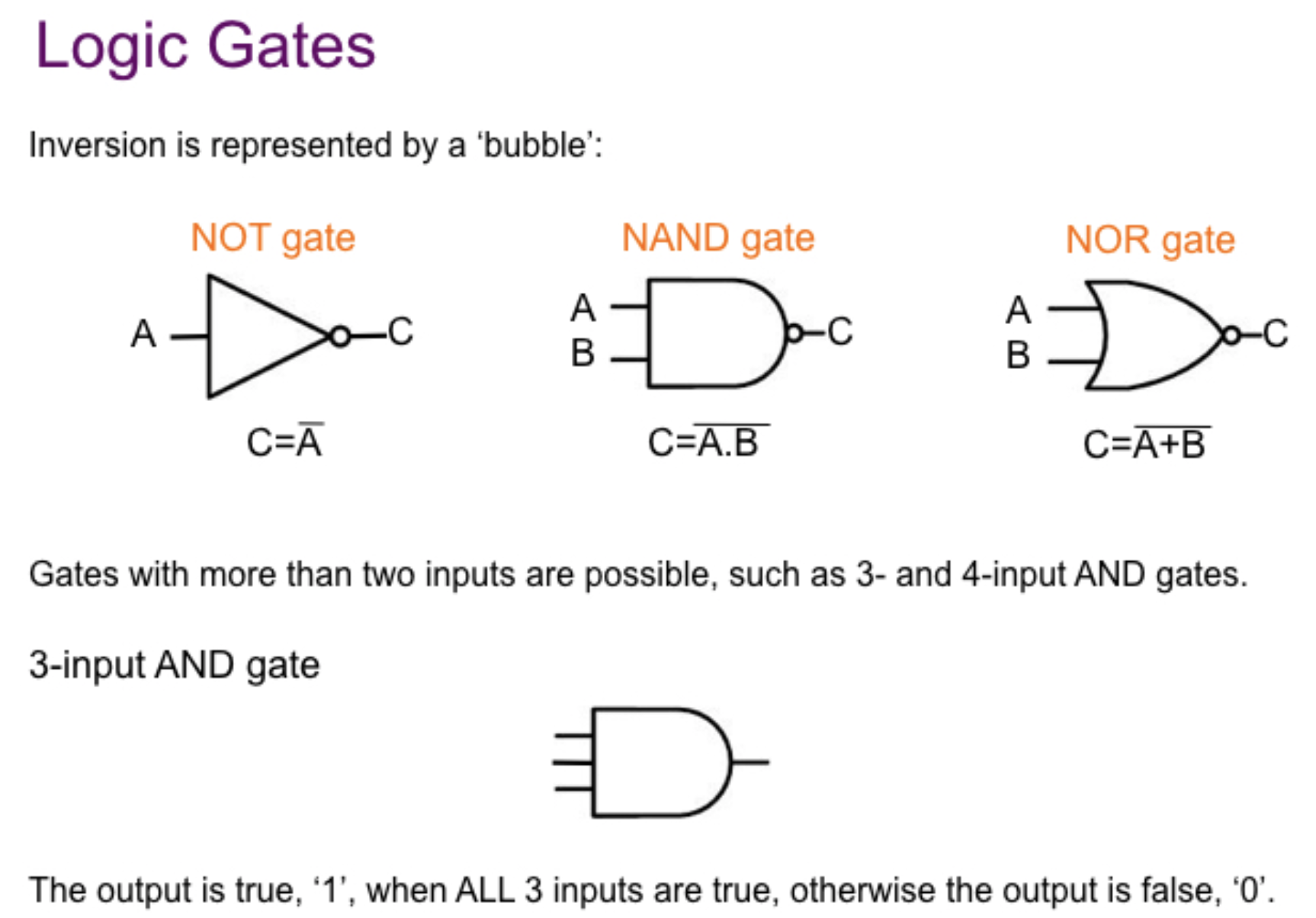
另外一种常见的电路设备是 多选器 Mux:
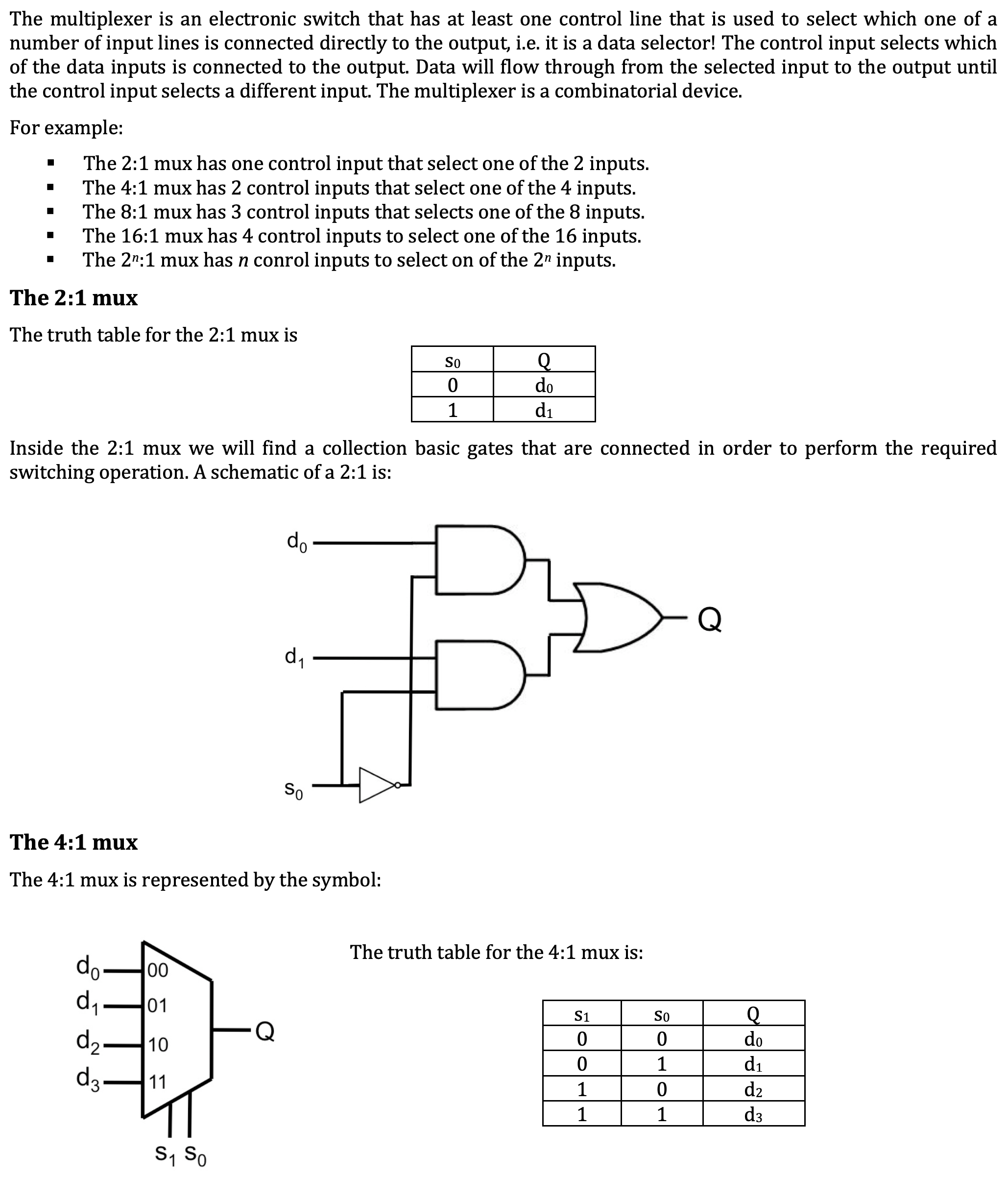
4. 抽象和分级设计思想
抽象和分级的设计思想在复杂系统的设计流程中极为常见. 计算机芯片作为极其复杂的系统, 也在其设计流程中涉及了这样的思想.
4.1 抽象设计思想
抽象 Abstraction 设计思想的核心是隐藏一些基础性或重复性的细节构造, 设计者因而无需关注一些设计的细节, 而专注于更高级别的设计与构造. 如: 在设计处理器时, 通过将逻辑门电路抽象化, 我们可以专注于寄存器, ALU, 控制模块与总线的构造.
4.2 分级设计思想
分级设计思想的核心是将一组不同的模块或元素按照复杂度, 重要性, 规模等指标对其进行排列.
5. 时序系统
输出由且仅由输入的值和电路本身所决定的电路被称为 组合逻辑电路 (Combinatorial Circuits). 另一种输出值还会受时序所影响的电路就是 时序逻辑电路 (Sequential Systems).
5.1 时钟
对时序系统而言, 其输出同时受时序 (或称: 受此前所接受的输入) 所影响. 在数字电路中, 我们使用 时钟信号 确定时序的正常运行.
时钟信号是一种固定地, 周期性地连续在高电平和低电平两种状态之间来回变换的无限信号流 (infinite stream of pulses).


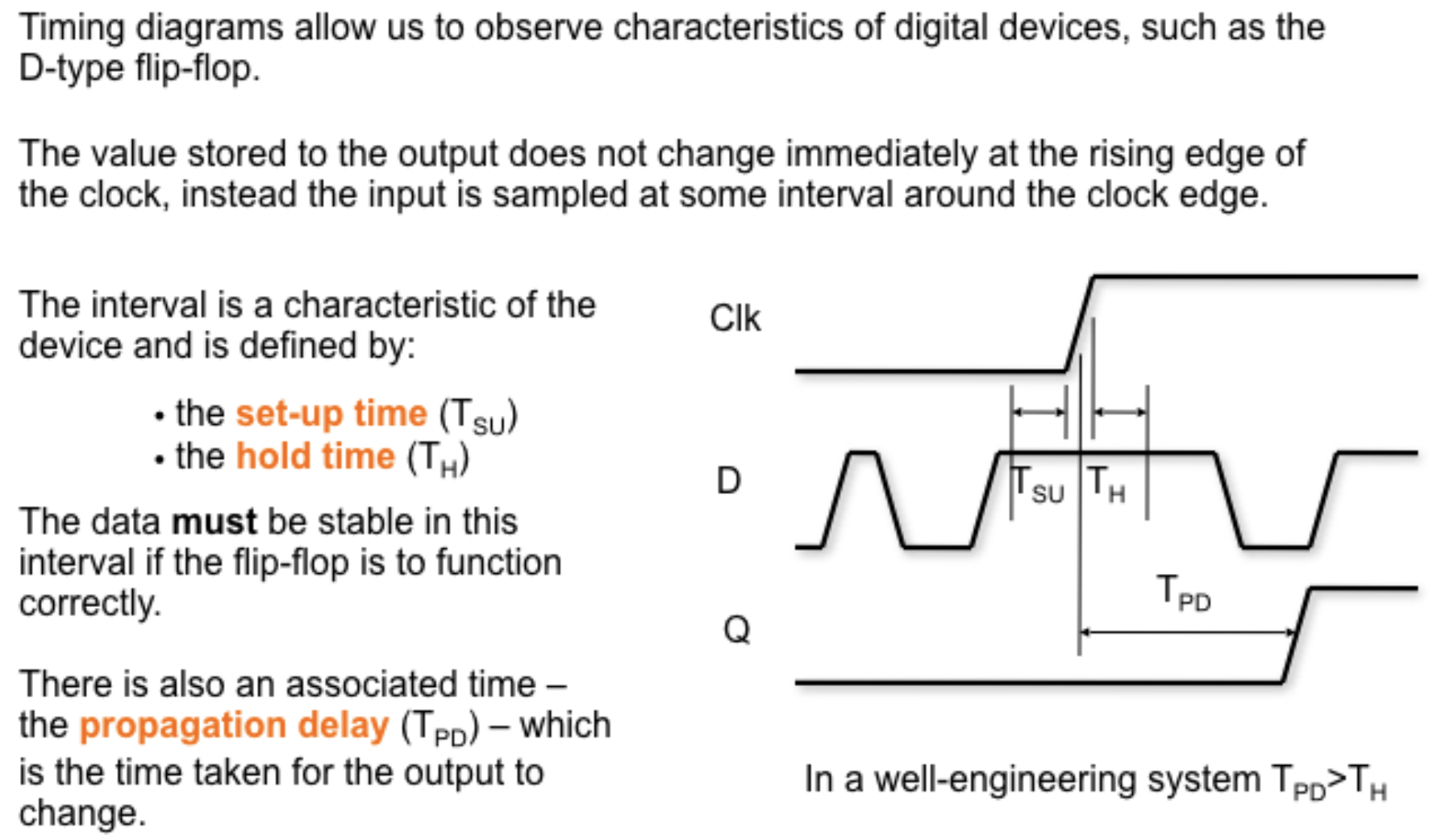
5.2 触发器

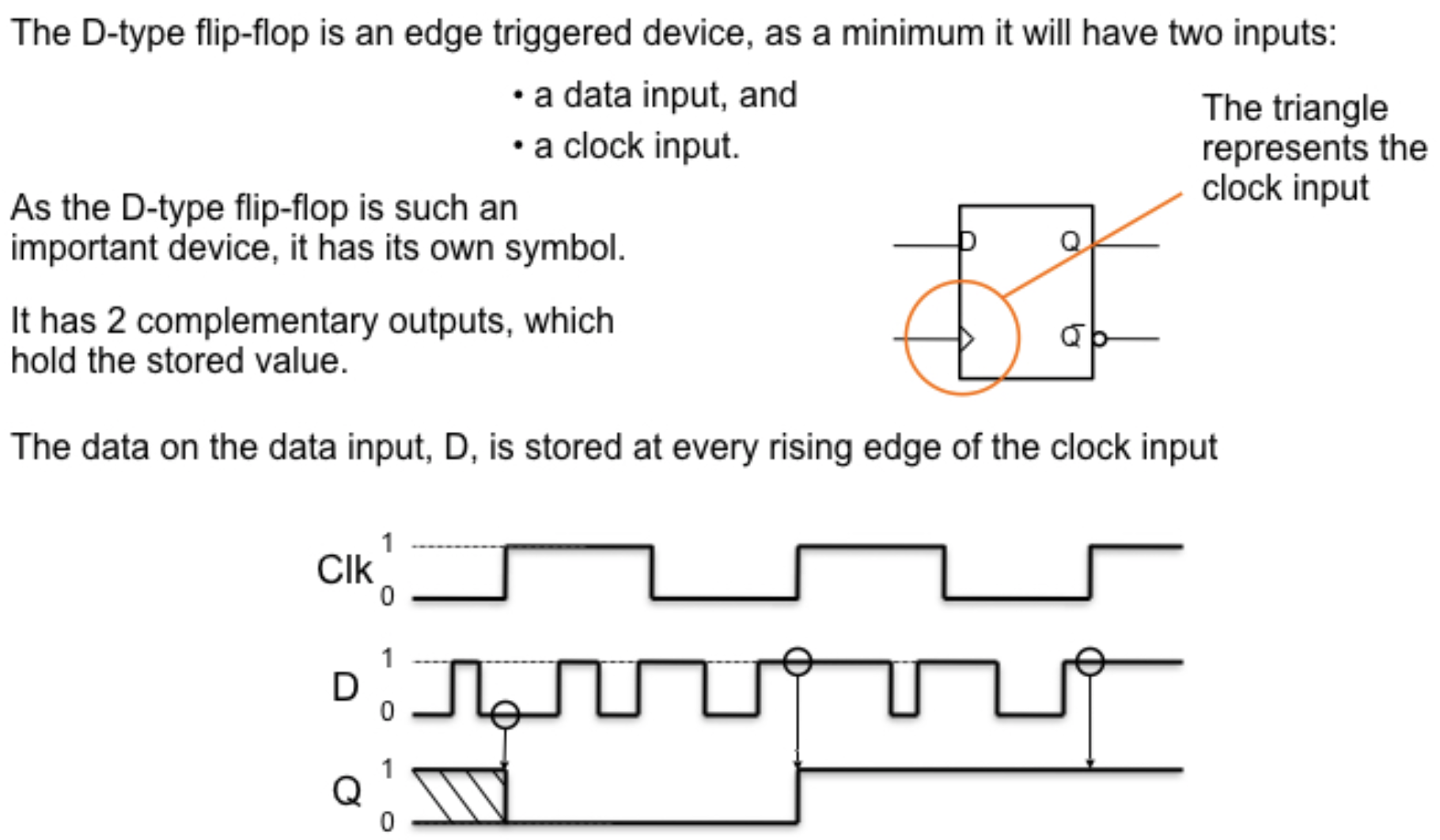
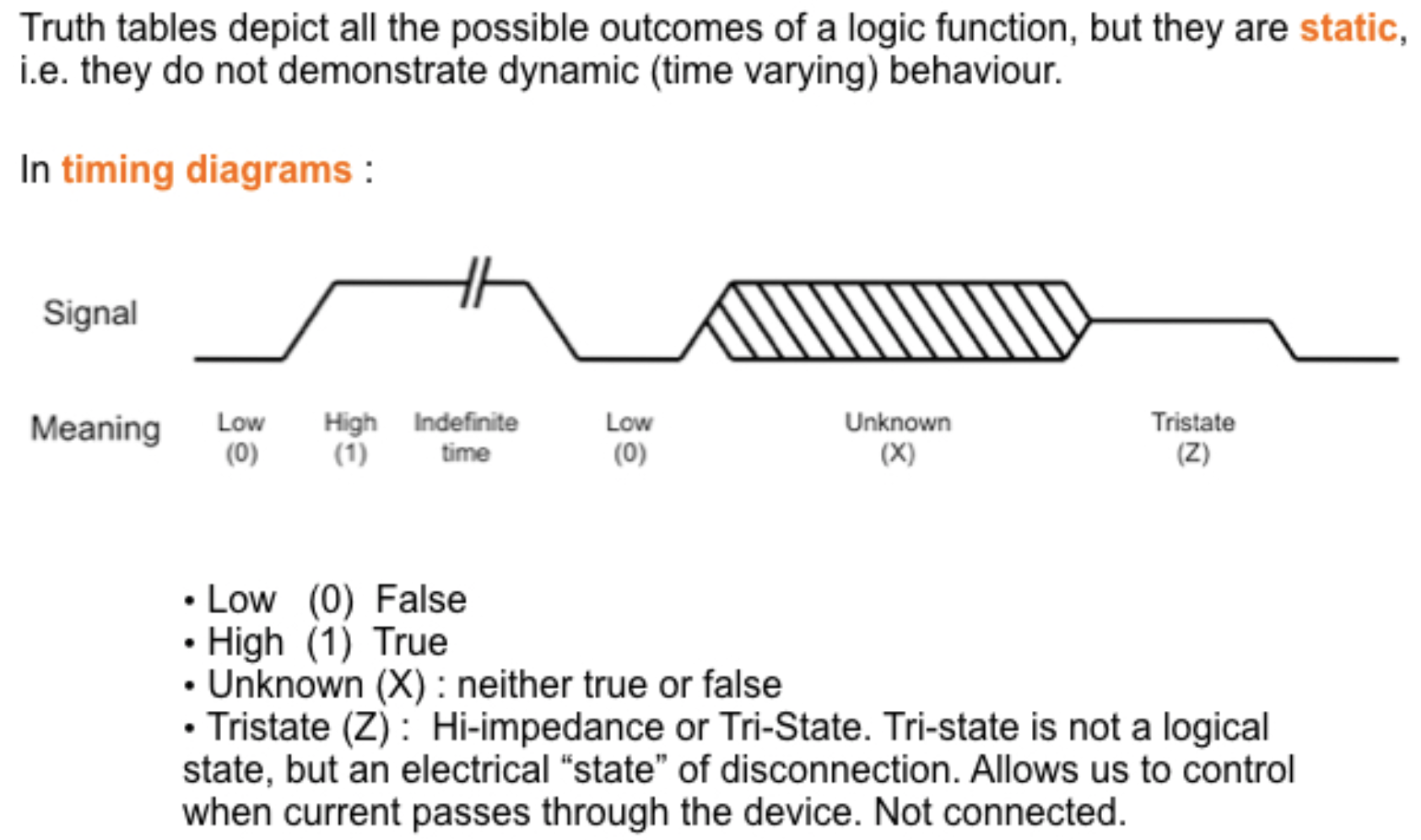
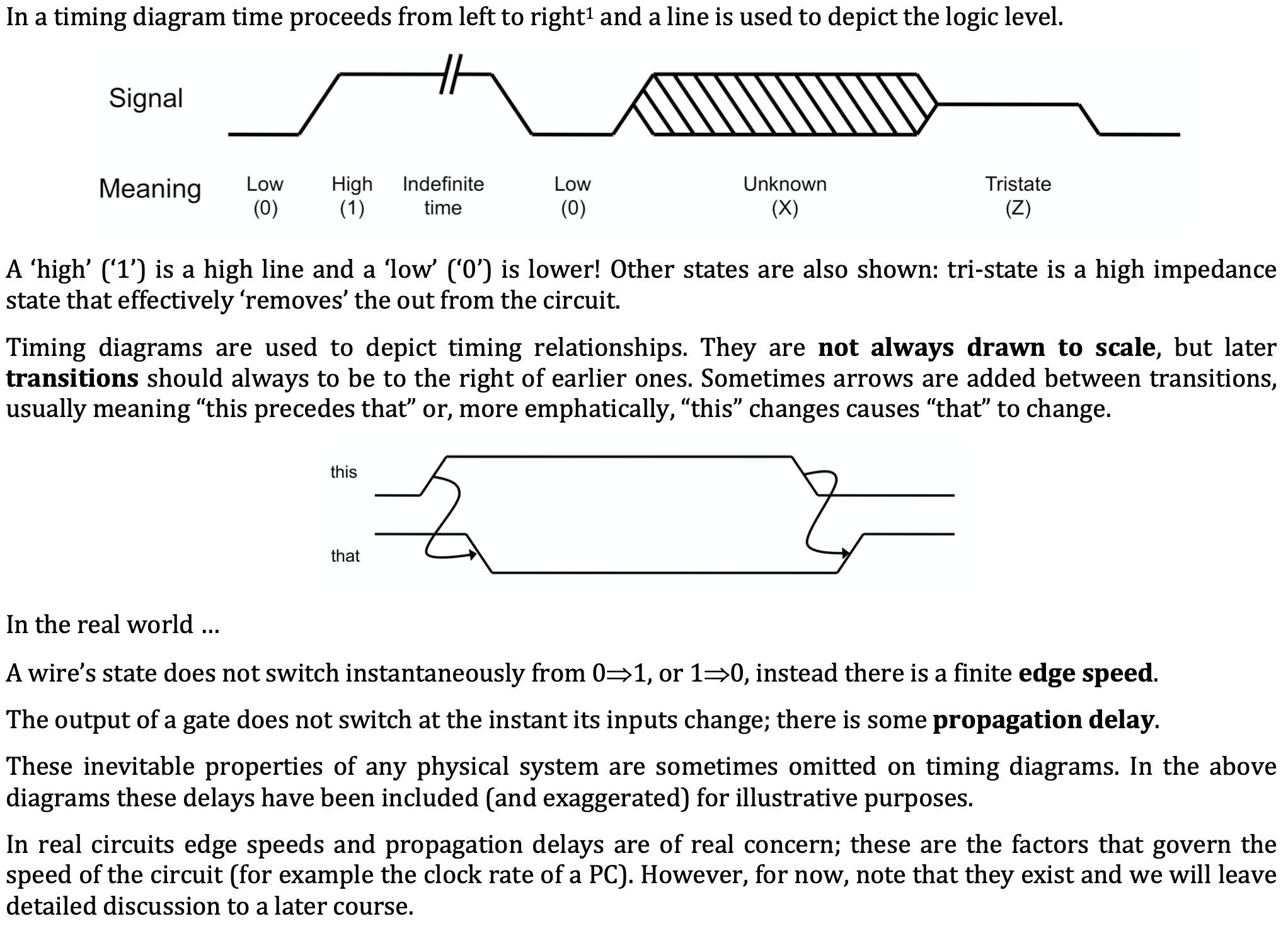
5.3 时序图